
| A. | 0 | B. | 3 | C. | 4 | D. | 5 |
分析 求出f(x)的导数,问题转化为方程x2+(2+a)x+a+b=0有两个不相同的实数根,结合二次函数的性质判断即可.
解答 解:函数f(x)有两个不相同的极值点,
即f′(x)=ex[x2+(2+a)x+a+b]=0有两个不相同的实数根x1,x2,
也就是方程x2+(2+a)x+a+b=0有两个不相同的实数根,
所以△=(2+a)2-4(a+b)>0;
由于方程f2(x)+(2+a)f(x)+a+b=0的判别式△′=△,
故此方程的两个解为f(x)=x1或f(x)=x2.
由于函数y=f(x)的图象和直线y=x1的交点个数即为方程f(x)=x1的解的个数,
函数y=f(x)的图象和直线y=x2的交点个数即为方程f(x)=x2的解的个数.
根据函数的单调性以及f(x1)=x1,
可知y=f(x)的图象和直线y=x1的交点个数为2,
y=f(x)的图象和直线y=x2的交点个数为1.
所以f(x)=x1或f(x)=x2共有三个不同的实数根,
即关于x的方程f2(x)+(2+a)f(x)+a+b=0的不同实根个数为3,
故选:B.
点评 本题难度中等偏上,是导数单调性、极值点与解一元 二次方程的综合题目,求解的关键是判断出函数的单调性,并将方程解的个数问题转化为函数图象的交点个数问题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | (¬p)∨(¬q) | C. | p∨q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,$\sqrt{{3^{x_0}}+1}$>1 | B. | ?x0∈R,$\sqrt{{3^{x_0}}+1}$≥1 | C. | ?x∈R,$\sqrt{{3^{x_0}}+1}$>1 | D. | ?x∈R,$\sqrt{{3^{x_0}}+1}$<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
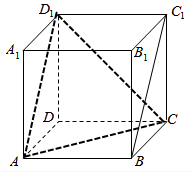 如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,平面AD1C把正方体分成两部分.求:
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,平面AD1C把正方体分成两部分.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2.
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com