
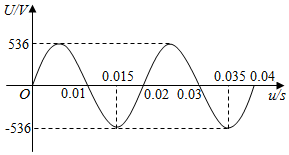
 一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式.
一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式. 分析 根据条件设U=Asin(ωt+φ),根据图象求出A,ω和φ的值即可得到结论.
解答 解:设U=Asin(ωt+φ),则A=536,
函数的周期T=0.02=$\frac{2π}{ω}$,则ω=100π,
即U=536sin(100πt+φ),
∵当t=0.015,U=-536,
∴-536=536sin(100π×0.015+φ),
即sin(1.5π+φ)=-1,
则1.5π+φ=$\frac{3π}{2}$+2kπ,
即φ=2kπ,
则U=536sin(100πt+2kπ)=536sin(100πt).
点评 本题主要考查三角函数解析式的求解,根据条件确定条件,求出A,ω和φ的值是解决本题的关键.


科目:高中数学 来源: 题型:解答题
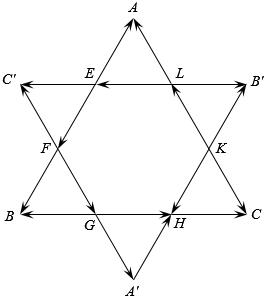 如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:
如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(x+1)cosx-sinx}{{(x+1)}^{2}}$ | B. | $\frac{(x+1)sinx-cosx}{x+1}$ | ||
| C. | $\frac{(x+1)sinx-cosx}{{(x+1)}^{2}}$ | D. | $\frac{(x+1)sinx+cosx}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x≥-2} | C. | {x|0≤x≤1} | D. | {x|-4≤x≤0且x≠-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,f(x0)≥g(x0)≥h(x0) | B. | ?x0∈R,f(x0)≥g(x0)或g(x0)≥h(x0) | ||
| C. | ?x∈R,f(x)≥g(x)≥h(x) | D. | ?x∈R,f(x)≥g(x)或g(x)≥h(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{5}$,$\frac{9}{5}$) | B. | (-$\frac{2}{5}$,$\frac{9}{5}$) | C. | ($\frac{2}{5}$,-$\frac{9}{5}$) | D. | (-$\frac{2}{5}$,-$\frac{9}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com