
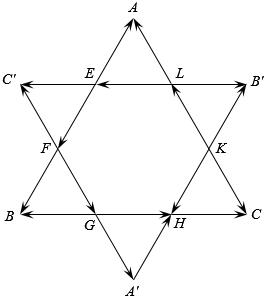
 如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:
如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:分析 (1)利用相等向量的定义即可得出;
(2)利用共线向量的定义即可得出;
(3)利用平行向量的定义即可得出.
解答 解:(1)与$\overrightarrow{GH}$相等的向量:$\overrightarrow{L{B}^{′}}$,$\overrightarrow{HC}$.
(2)与$\overrightarrow{GH}$共线的向量:$\overrightarrow{L{B}^{′}}$,$\overrightarrow{HC}$,$\overrightarrow{E{C}^{′}}$,$\overrightarrow{LE}$,$\overrightarrow{GB}$.
(3)与$\overrightarrow{EA}$平行的向量:$\overrightarrow{EF}$,$\overrightarrow{FB}$,$\overrightarrow{K{B}^{′}}$,$\overrightarrow{KH}$,$\overrightarrow{{A}^{′}H}$.
点评 本题考查了相等向量、共线向量与平行向量的定义,考查了推理能力与计算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{{e}^{3}}{4}$,0) | B. | [-$\frac{e}{2}$,0) | C. | [-$\frac{{e}^{3}}{4}$,$\frac{e}{2}$) | D. | [-$\frac{{e}^{3}}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
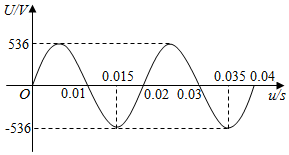 一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式.
一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com