
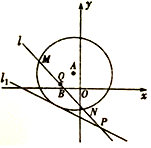
 如图所示,已知圆A的圆心在直线y=-2x上,且该圆存在两点关于直线x+y-1=0对称,又圆A与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知圆A的圆心在直线y=-2x上,且该圆存在两点关于直线x+y-1=0对称,又圆A与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.分析 (1)设出圆A的半径,根据以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.点到直线的距离等于半径,我们可以求出圆的半径,进而得到圆的方程;
(2)根据半弦长,弦心距,圆半径构成直角三角形,满足勾股定理,我们可以结合直线l过点B(-2,0),求出直线的斜率,进而得到直线l的方程;
(3)由直线l过点B(-2,0),我们可分直线的斜率存在和不存在两种情况,分别讨论($\overrightarrow{BM}$+$\overrightarrow{BN}$)•$\overrightarrow{BP}$是否为定值,综合讨论结果,即可得到结论.
解答 解:(1)由圆存在两点关于直线x+y-1=0对称知圆心A在直线x+y-1=0上,
由$\left\{{\begin{array}{l}{y=-2x}\\{x+y-1=0}\end{array}}\right.$得A(-1,2),
设圆A的半径为R,因为圆A与直线l1:x+2y+7=0相切,
∴$R=\frac{{|{-1+4+7}|}}{{\sqrt{5}}}=2\sqrt{5}$,
∴圆A的方程为(x+1)2+(y-2)2=20,
(2)当直线l与x轴垂直时,易知x=-2符合题意,
当直线l与x轴不垂直时,设直线l的方程为y=k(x+2),
即kx-y+2k=0连接AQ,则AQ⊥MN,
∵$|{MN}|=2\sqrt{19}$,∴$|{AQ}|=\sqrt{20-19}=1$,
由$|{AQ}|=\frac{{|{k-2}|}}{{\sqrt{{k^2}+1}}}=1$,得$k=\frac{3}{4}$,
∴直线l的方程为3x-4y+6=0,
∴所求直线l的方程为x=-2或3x-4y+6=0,
(3)∵AQ⊥BP,∴$\overrightarrow{AQ}$•$\overrightarrow{BP}$=0,
∴($\overrightarrow{BM}$+$\overrightarrow{BN}$)•$\overrightarrow{BP}$=2$\overrightarrow{BQ}$•$\overrightarrow{BP}$=2($\overrightarrow{BA}+\overrightarrow{AQ}$)•$\overrightarrow{BP}$=2($\overrightarrow{BA}•\overrightarrow{BP}$+$\overrightarrow{AQ}$•$\overrightarrow{BP}$)=2$\overrightarrow{BA}$•$\overrightarrow{BP}$,
当直线l与x轴垂直时,得$P[{-2,-\frac{5}{2}}]$,则$\overrightarrow{BP}$=(0,$\frac{5}{2}$),又$\overrightarrow{BA}$=(1,2),
∴($\overrightarrow{BM}$+$\overrightarrow{BN}$)•$\overrightarrow{BP}$=2$\overrightarrow{BQ}$•$\overrightarrow{BP}$=2$\overrightarrow{BA}$•$\overrightarrow{BP}$=0,
当直线l的斜率存在时,设直线l的方程为y=k(x+2),
由$\left\{{\begin{array}{l}{y=kx+2}\\{x+2y+7=0}\end{array}}\right.$,解得$P[{\frac{-4k-7}{1+2k},\frac{-5k}{1+2k}}]$,∴$\overrightarrow{BP}$=($\frac{-5}{1+2k}$,$\frac{-5k}{1+2k}$),
∴($\overrightarrow{BM}$+$\overrightarrow{BN}$)•$\overrightarrow{BP}$=2$\overrightarrow{BQ}$•$\overrightarrow{BP}$=2$\overrightarrow{BA}$•$\overrightarrow{BP}$=2($\frac{-5}{1+2k}$+$\frac{-5k}{1+2k}$)=-10
综上所述,($\overrightarrow{BM}$+$\overrightarrow{BN}$)•$\overrightarrow{BP}$是定值,且为-10
点评 本题考查的知识点是直线和圆的方程的应用,直线的一般式方程,圆的标准方程,其中(1)的关键是求出圆的半径,(2)的关键是根据半弦长,弦心距,圆半径构成直角三角形,满足勾股定理,求出弦心距(即圆心到直线的距离),(3)中要注意讨论斜率不存在的情况,这也是解答直线过定点类问题的易忽略点.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )| A. | -0.6 | B. | -0.69 | C. | -0.7 | D. | -0.71 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
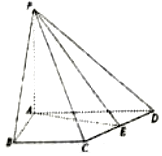 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
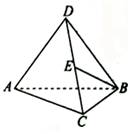 如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )
如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{16}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com