
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小
的距离小![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() .设线段
.设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由题意可知:动点![]() 到定点
到定点![]() 的距离等于
的距离等于![]() 到定直线
到定直线![]() 的距离,由此利用抛物线的定义能求出点
的距离,由此利用抛物线的定义能求出点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)设![]() 两点坐标分别为
两点坐标分别为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .由题意可设直线
.由题意可设直线![]() 的方程为
的方程为![]() ,
,![]() ,由
,由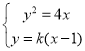 ,得
,得![]() .由此利用根的判别式、韦达定理、直线的斜率、直线方程,结合已知条件能证明直线
.由此利用根的判别式、韦达定理、直线的斜率、直线方程,结合已知条件能证明直线![]() 恒过定点
恒过定点![]() .
.
(3)求出![]() ,利用基本不等式能求出三角形面积的最小值.
,利用基本不等式能求出三角形面积的最小值.
解:(1)由题意可知:动点![]() 到定点
到定点![]() 的距离等于
的距离等于![]() 到定直线
到定直线![]() 的距离.根据抛物线的定义可知,点
的距离.根据抛物线的定义可知,点![]() 的轨迹
的轨迹![]() 是抛物线.
是抛物线.
![]() ,
,![]() 抛物线方程为:
抛物线方程为:![]()
(2)设![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由题意可设直线![]() 的方程为
的方程为![]()
![]() .
.
由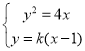 ,得
,得![]() .
.
![]() .
.
因为直线![]() 与曲线
与曲线![]() 于
于![]() ,
,![]() 两点,所以
两点,所以![]() ,
,![]() .
.
所以点![]() 的坐标为
的坐标为![]() .由题知,直线
.由题知,直线![]() 的斜率为
的斜率为![]() ,同理可得点
,同理可得点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,有
时,有![]() ,此时直线
,此时直线![]() 的斜率
的斜率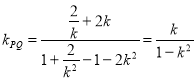 .
.
所以,直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
于是,直线![]() 恒过定点
恒过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,也过点
,也过点![]() .
.
综上所述,直线![]() 恒过定点
恒过定点![]() .
.
(3)可求得![]() .所以
.所以![]() 面积
面积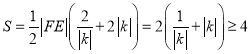 .
.
当且仅当![]() 时,“
时,“![]() ”成立,所以
”成立,所以![]() 面积的最小值为
面积的最小值为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,若
,若![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程与离心率;
的方程与离心率;
(2)过点![]() 做直线
做直线![]() 与椭圆
与椭圆![]() 相交于两个不同的点
相交于两个不同的点![]() ;若
;若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
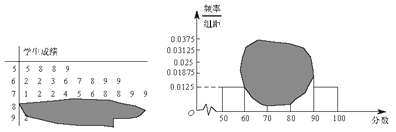
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高的(不超过三次)多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
,![]() 依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线
依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
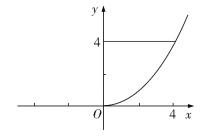
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com