
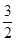 与x=-1时有极值.
与x=-1时有极值.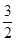 )
) 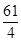 ,最大值为16.
,最大值为16.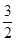 )=0,解出a、b的值,进而求出解析式
)=0,解出a、b的值,进而求出解析式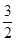 与x =-1时函数有极值.
与x =-1时函数有极值.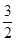 与x =-1满足f ¢(x)=0.
与x =-1满足f ¢(x)=0.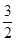 ,+∞)均为函数的单调递增区间;
,+∞)均为函数的单调递增区间;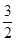 )为函数的单调递减区间. ……8分
)为函数的单调递减区间. ……8分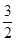 ) 均属于[-1,2],?
) 均属于[-1,2],?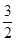 )=-
)=-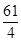 , ……10分
, ……10分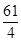 ,最大值为16. ……12分
,最大值为16. ……12分

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com