练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (本小题满分12分)
    在△ABC中，角A、B、C的对边分别为、、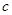，且满足．
    （1）求角B的大小；

    20070316

     
    （2）设，求的最小值．

    (1) (2) 当时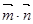，取得最小值0．

    解析试题分析：解：（1）由正弦定理，有 ， ，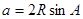
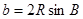    代入(2a－c)cosB=bcosC，得（2sinA－sinC）cosB="sinBcosC."
    即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
    ∵A+B+C=π，∴2sinAcosB="sinA."
    ∵0<A<π,∴sinA≠0.
    ∴cosB=.
    ∵0<B<π，∴B=.
    （2）=－sinA+1
    由B=得A∈（0，）
    所以，当时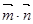，取得最小值0．
    考点：解三角形
    点评：解决的关键是根据已知的边角关系化简变形，结合正弦定理和来得到结论，同时结合向量的数量积来求解最值，属于基础题。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    在△ABC中，角A，B，C所对的边长分别是a，b，c．（1）若sin C + sin（B－A）=" sin" 2A，试判断△ABC的形状；（2）若△ABC的面积S = 3，且c =，C =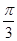，求a，b的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某货轮在A处看灯塔B在货轮的北偏东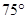的方向上，距离为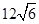海里，在A处看灯塔C在货轮的北偏西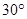的方向上，距离为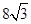海里，货轮由A处向正北航行到D处时，再看灯塔B在南偏东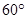方向上，求：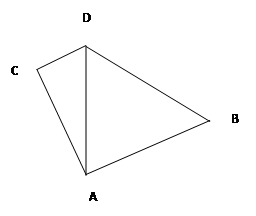

    （1）AD的距离；
    （2）CD的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知平面直角坐标系中,顶点的分别为，其中．
    （1）若，求的值；
    （2）若，求周长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题满分12分) 在中，分别是角的对边，，.
    （Ⅰ）求的值；
    （Ⅱ）若，求边的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中，内角对边的边长分别是，已知，．
    （Ⅰ）若的面积等于，求；
    （Ⅱ）若，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分） 已知的角A、B、C所对的边分别是，
    设向量, ,
    （Ⅰ）若∥，求证：为等腰三角形；
    （Ⅱ）若⊥，边长，，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数（）的最小正周期为，
    （Ⅰ）当时，求函数的最小值；
    （Ⅱ）在中，若,且,求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分10分）如图，，，，在线段上任取一点，

    试求：(1)为钝角三角形的概率；
    (2)为锐角三角形的概率．

    查看答案和解析>>

    同步练习册答案