
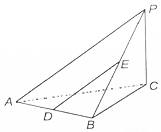
 如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.
如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.分析 (1)证明DE∥PA,利用线面平行的判定定理,证明DE∥平面PAC;
(2)证明AB⊥平面PBC,即可证明:AB⊥PB;
(3)若PC=BC=2,利用三棱锥的体积公式求三棱锥P-ABC的体积.
解答 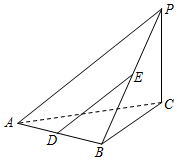 (1)证明:因为D,E分别是AB,PB的中点,
(1)证明:因为D,E分别是AB,PB的中点,
所以DE∥PA.
因为PA⊆平面PAC,且DE?平面PAC,
所以DE∥平面PAC. …(4分)
(2)证明:因为PC⊥平面ABC,且AB⊆平面ABC,
所以AB⊥PC.又因为AB⊥BC,且PC∩BC=C.
所以AB⊥平面PBC.又因为PB⊆平面PBC,
所以AB⊥PB. …(8分)
$\begin{array}{l}(3)∵PC⊥ABC,△ABC∠ABC={90°},AB=BC=2\\∴{V_{P-ABC}}=\frac{1}{3}{S_{△ABC}}•PC=\frac{1}{3}×(\frac{1}{2}×2×2)×2=\frac{4}{3}\end{array}$…(12分)
点评 本题考查线面平行、垂直的判定,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
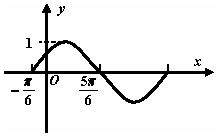 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象如图所示,则下列关于函数 f (x)的说法中正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象如图所示,则下列关于函数 f (x)的说法中正确的是( )| A. | 对称轴方程是x=$\frac{π}{6}$+kπ(k∈Z) | B. | 对称中心坐标是($\frac{π}{3}$+kπ,0)(k∈Z) | ||
| C. | 在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增 | D. | 在区间(-π,-$\frac{2π}{3}$)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,b?β,α∥β | B. | a∥α,b?β | C. | a⊥α,b⊥α | D. | a⊥α,b?α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{y}^{2}}{3}$-x2=1 | D. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
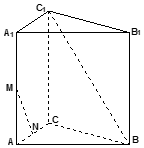 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com