
【题目】在△ABC中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,c.已知
,c.已知![]() .
.
则角![]() 的大小________
的大小________
【答案】![]() ;
;
【解析】分析:根据余弦定理,将题中等式化简整理,可得sinBcosC=2sinAcosB﹣sinCcosB,利用两角和正弦公式化简得2sinAcosB=sin(B+C)=sinA,在两边约去sinA得![]() ,结合三角形内角取值范围即可得到角B的大小.
,结合三角形内角取值范围即可得到角B的大小.
详解:∵在△ABC中,b2=a2+c2﹣2accosB,
∴b2﹣a2﹣c2=﹣2accosB,同理可得c2﹣a2﹣b2=﹣2abcosC
∵![]()
∴![]() ,
,
∵sinC≠0,可得sinBcosC=2sinAcosB﹣sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,
∵sinA≠0,∴等式两边约去sinA,可得![]() ,
,
∵0<B<π,∴角B的大小![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆否命题为:“若
”的逆否命题为:“若 ![]() ,则
,则 ![]() ”
”
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.若 ![]() 且
且 ![]() 为假命题,则
为假命题,则 ![]() 、
、 ![]() 均为假命题
均为假命题
D.命题 ![]() :“
:“ ![]() ,使得
,使得 ![]() ”,则
”,则 ![]() :“
:“ ![]() ,均有
,均有 ![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数为( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分条件;
③命题“若m≤ ![]() ,则方程mx2+2x+2=0有实数根”的否命题为真命题.
,则方程mx2+2x+2=0有实数根”的否命题为真命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() (a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+
(a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+ ![]() ,则该双曲线的离心率取值范围是( )
,则该双曲线的离心率取值范围是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对新研发的一种产品进行试销,得到如下数据表:
(1)根据上表求出回归直线方程 ![]() ,并预测当单价定为8.3元时的销量;
,并预测当单价定为8.3元时的销量;
(2)如果该工厂每件产品的成本为5.5元,利用所求的回归方程,要使得利润最大,单价应该定为多少?
附:线性回归方程 ![]() 中斜率和截距最小二乘估计计算公式:
中斜率和截距最小二乘估计计算公式: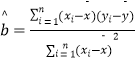 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水仙花经营部每天的房租、水电、人工等固定成本为1000元,每盆水仙花的进价是10元,销售单价![]() (元) (
(元) (![]() )与日均销售量
)与日均销售量![]() (盆)的关系如下表,并保证经营部每天盈利.
(盆)的关系如下表,并保证经营部每天盈利.
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
(Ⅰ) 在所给的坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定
的对应点,并确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(Ⅲ)请写出该经营部的日销售利润![]() 的表达式,并回答该经营部怎样定价才能获最大日销售利润?
的表达式,并回答该经营部怎样定价才能获最大日销售利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com