
【题目】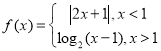 ,
,![]() ,若
,若![]() 有9个零点,则
有9个零点,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】过点P(3,﹣4)作圆(x﹣1)2+y2=2的切线,切点分别为A,B,则直线AB的方程为( )
A.x+2y﹣2=0B.x﹣2y﹣1=0C.x﹣2y﹣2=0D.x+2y+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() (其中
(其中![]() ):①若函数
):①若函数![]() 的一个对称中心到与它最近一条对称轴的距离为
的一个对称中心到与它最近一条对称轴的距离为![]() ,则
,则![]() ;②若函数
;②若函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的范围为
的范围为![]() ;③若
;③若![]() ,则
,则![]() 在点
在点![]() 处的切线方程为
处的切线方程为 ![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的最小值为
的最小值为![]() ;⑤若
;⑤若![]() ,则函数
,则函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象.其中正确命题的序号有_______.(把你认为正确的序号都填上)
的图象.其中正确命题的序号有_______.(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() 在平面直角坐标系
在平面直角坐标系![]() 中,已知点
中,已知点![]() 直线
直线![]() 曲线
曲线![]() 与
与![]() 轴交于点A与
轴交于点A与![]() 交于点
交于点![]() 分别是曲线
分别是曲线![]() 与线段AB上的动点.
与线段AB上的动点.
(1)用![]() 表示点B到点F的距离;
表示点B到点F的距离;
(2)若![]() 且
且![]() 求
求![]() 的值;
的值;
(3)设![]() 且存在点P、Q,使得
且存在点P、Q,使得![]() 是等边三角形,求
是等边三角形,求![]() 的边长.
的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
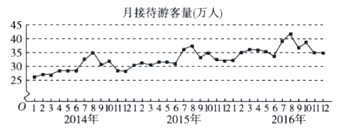
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,小明为了帮助爸爸戒烟,在爸爸包里放一个小盒子,里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”,并且和爸爸约定,每次想吸烟时,从盒子里任取一支,若取到口香糖则吃一支口香糖,不吸烟;若取到香烟,则吸一支烟,不吃口香糖,假设每次香烟和口香糖被取到的可能性相同,则“口香糖吃完时还剩2支香烟”的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为-2,
的最小值为-2,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象过点
的图象过点![]() .
.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)若![]() 函数
函数![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com