
【题目】对于函数![]() (其中
(其中![]() ):①若函数
):①若函数![]() 的一个对称中心到与它最近一条对称轴的距离为
的一个对称中心到与它最近一条对称轴的距离为![]() ,则
,则![]() ;②若函数
;②若函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的范围为
的范围为![]() ;③若
;③若![]() ,则
,则![]() 在点
在点![]() 处的切线方程为
处的切线方程为 ![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的最小值为
的最小值为![]() ;⑤若
;⑤若![]() ,则函数
,则函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象.其中正确命题的序号有_______.(把你认为正确的序号都填上)
的图象.其中正确命题的序号有_______.(把你认为正确的序号都填上)
【答案】①④
【解析】
①根据条件,可得![]() ,然后利用周期公式求出
,然后利用周期公式求出![]() ;②根据
;②根据![]() 在
在![]() 上单调递增,可得
上单调递增,可得 ,然后求出
,然后求出![]() 的范围;③当
的范围;③当![]() 时,求出f(0)和f(x)的导函数,然后求出
时,求出f(0)和f(x)的导函数,然后求出![]() 处的切线方程的斜率
处的切线方程的斜率![]() ,再求出切线方程即可;④根据
,再求出切线方程即可;④根据![]() ,直接利用整体法求出f(x)的值域,从而得到f(x)的最小值;⑤直接求出函数
,直接利用整体法求出f(x)的值域,从而得到f(x)的最小值;⑤直接求出函数![]() 的图象向右平移
的图象向右平移![]() 个单位的解析式即可.
个单位的解析式即可.
解:①若函数![]() 的一个对称中心到与它最近一条对称轴的距离为
的一个对称中心到与它最近一条对称轴的距离为![]() ,则
,则
![]() ,所以
,所以![]() ,所以
,所以![]() ,故①正确;
,故①正确;
②当![]() ,则
,则![]() ,
,
因为![]() ,所以若函数
,所以若函数![]() 在
在![]() 上单调递增,则
上单调递增,则 ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,故②错误;
,故②错误;
③当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,所以切线的斜率
,所以切线的斜率![]() ,
,
所以![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,故③错误;
,故③错误;
④当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() ,所以
,所以![]() ,故④正确;
,故④正确;
⑤当![]() 时,
时,![]() ,若
,若![]() 的图象向右平移
的图象向右平移![]() 个单位,
个单位,
则![]() ,故⑤错误.
,故⑤错误.
故答案为:①④.


科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.

(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4-4:坐标系与参数方程
已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为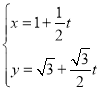 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴正半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点P(x,y)的坐标满足![]() (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线l的极坐标方程为ρsin(θ+φ)=cosφ(其中φ为常数,且φ
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线l的极坐标方程为ρsin(θ+φ)=cosφ(其中φ为常数,且φ![]() )
)
(1)求动点P的轨迹C的极坐标方程;
(2)设直线l与轨迹C的交点为A,B,两点,求证:当φ变化时,∠AOB的大小恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为落实国家扶贫攻坚政策,某社区应上级扶贫办的要求,对本社区所有扶贫户每年年底进行收入统计,下表是该社区扶贫户中![]() 户从2016年至2019年的收入统计数据:(其中
户从2016年至2019年的收入统计数据:(其中![]() 为
为![]() 贫困户的人均年纯收人)
贫困户的人均年纯收人)
年份 | 2016年 | 2017年 | 2018年 | 2019年 |
年份代码 |
|
|
|
|
人均纯收入 |
|
|
|
|
(1)作出贫困![]() 户的人均年纯收人的散点图;
户的人均年纯收人的散点图;
(2)根据上表数据,用最小二乘法求出![]() 关于年份代码
关于年份代码![]() 的线性回归方程
的线性回归方程![]() ,并估计
,并估计![]() 贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于
贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于![]() 元)
元)
(参考公式: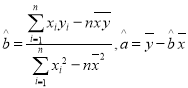 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 为抛物线上不重合的两动点,
为抛物线上不重合的两动点,![]() 为坐标原点,
为坐标原点,![]() ,过
,过![]() ,
,![]() 作抛物线的切线
作抛物线的切线![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求抛物线的方程;
(2)问:直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由;
是否过定点,若是,求出定点坐标,若不是,说明理由;
(3)三角形![]() 的面积是否存在最小值,若存在,请求出最小值.
的面积是否存在最小值,若存在,请求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线P:![]() 的焦点为F,经过点
的焦点为F,经过点![]() 作直线与抛物线P相交于A,B两点,设
作直线与抛物线P相交于A,B两点,设![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)是否存在常数a,当点M在抛物线P上运动时,直线![]() 都与以MF为直径的圆相切?若存在,求出所有a的值;若不存在,请说明理由.
都与以MF为直径的圆相切?若存在,求出所有a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com