练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校要在一条水泥路边安装路灯，其中灯杆的设计如图所示，AB为地面，CD，CE为路灯灯杆，CD⊥AB，∠DCE=，在E处安装路灯，且路灯的照明张角∠MEN=.已知CD=4m，CE=2m.

    (1)当M，D重合时，求路灯在路面的照明宽度MN；

    (2)求此路灯在路面上的照明宽度MN的最小值.

    【答案】(1) ；(2) .

    【解析】

    （1）用余弦定理求出，进而求出，结合已知条件，求出，用正弦定理求出；

    （2）由面积公式，余弦定理结合基本不等式，即可求出结果.

    (1)当M，D重合时，

    由余弦定理知，

    ∴

    ∵

    ∴，

    ∵

    ∴

    ∵

    ∴在ΔEMN中，由正弦定理可知，

    解得；

    (2)易知E到地面的距离=5m

    由三角形面积公式可知，

    ∴，又由余弦定理可知，，

    当且仅当EM=EN时，等号成立，

    ∴，解得

    答:(1)路灯在路面的照明宽度为m；

    (2)照明宽度MV的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，过顶点的直线与椭圆相交于两点.

    （1）求椭圆的方程；

    （2）若点在椭圆上且满足，求直线的斜率的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

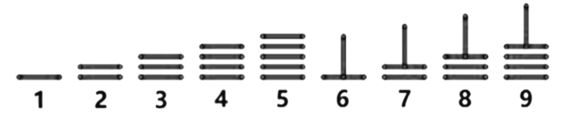
    【题目】中国古代十进制的算筹计数法，在数学史上是一个伟大的创造，算筹实际上是一根根同长短的小木棍.如图，是利用算筹表示1-9的一种方法.则据此，3可表示为“”，26可表示为“”，现有6根算筹，据此表示方法，若算筹不能剩余，则可以用1-9这9数字表示的两位数的个数为（ ）

    A.9B.13C.16D.18

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角中，角A，B，C所对边分别为a，b，c，已知．

    （1）求A ；

    （2）求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（），是自然对数的底数．

    （1）当时，求的单调增区间；

    （2）若对任意的，（），求的最大值；

    （3）若的极大值为，求不等式的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系中，曲线的参数方程为（为参数），直线的方程为．

    （1）以坐标原点为极点，轴的正半轴为极轴建立极坐标系，求曲线的极坐标方程和直线的极坐标方程；

    （2）在（1）的条件下，直线的极坐标方程为，设曲线与直线的交于点和点，曲线与直线的交于点和点，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面，，，分别为的中点．

    （Ⅰ）证明：平面平面；

    （Ⅱ）若，求平面与平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过点P(3,﹣4)作圆(x﹣1)2+y2＝2的切线，切点分别为A，B，则直线AB的方程为（　　 ）

    A.x+2y﹣2＝0B.x﹣2y﹣1＝0C.x﹣2y﹣2＝0D.x+2y+2＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数（其中）：①若函数的一个对称中心到与它最近一条对称轴的距离为，则；②若函数在上单调递增，则的范围为；③若，则在点处的切线方程为 ；④若，，则的最小值为；⑤若，则函数的图象向右平移个单位可以得到函数的图象.其中正确命题的序号有_______.（把你认为正确的序号都填上）

    查看答案和解析>>

    同步练习册答案