
【题目】已知椭圆![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的另一个焦点是
的另一个焦点是![]() ,且
,且![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD. 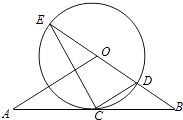
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,
轴正半轴为极轴,建立极坐标系,
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数,
是参数, ![]() ),以原点
),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() 时,曲线
时,曲线![]() 和
和![]() 相交于
相交于![]() 、
、![]() 两点,求以线段
两点,求以线段![]() 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=2,E为线段PD上一点,记 ![]() =λ. 当λ=
=λ. 当λ= ![]() 时,二面角D﹣AE﹣C的平面角的余弦值为
时,二面角D﹣AE﹣C的平面角的余弦值为 ![]() .
. 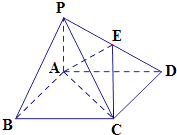
(1)求AB的长;
(2)当 ![]() 时,求异面直线BP与直线CE所成角的余弦值.
时,求异面直线BP与直线CE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ![]() ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 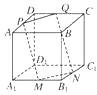
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN= ![]() π,在△ABC中,角A、B、C所对的边分别是a、b、c.
π,在△ABC中,角A、B、C所对的边分别是a、b、c.
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c= ![]() ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第12界全运会于2013年8月31日在辽宁沈阳顺利举行,组委会在沈阳某大学招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以下(不包括175
以下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.

(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程
在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 上两点
上两点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)设![]() 为线段
为线段![]() 上的动点,求线段
上的动点,求线段![]() 取得最小值时,点
取得最小值时,点![]() 的直角坐标;
的直角坐标;
(2)求以为![]() 为直径的圆
为直径的圆![]() 的参数方程,并求在(1)条件下直线
的参数方程,并求在(1)条件下直线![]() 与圆
与圆![]() 相交所得的弦长.
相交所得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com