练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知各项均不相等的等差数列的前五项和，且成等比数列.

    （1）求数列的通项公式；

    （2）若为数列的前项和，且存在，使得成立，求实数的取值范围.

    【答案】（1）；（2）.

    【解析】试题分析：（1）用基本量法，即用表示已知条件，列出方程组，求出即可求数列的通项公式；（2）用裂项相消法求数列的前项和，列出不等式参变分离得，由基本不等式求的最小值即可.

    试题解析： （1）设数列的公差为，则

    即………………2分

    又因为，所以………………4分

    所以.………………5分

    （2）因为，

    所以.………………7分

    因为存在，使得成立，

    所以存在，使得成立，

    即存在，使成立.………………9分

    又，（当且仅当时取等号），

    所以.

    即实数的取值范围是.………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在海岸处，发现北偏东方向，距离为海里的处有一艘走私船，在处北偏西方向，距离为海里的处有一艘缉私艇奉命以海里/时的速度追截走私船，此时，走私船正以海里/时的速度从处向北偏东方向逃窜.

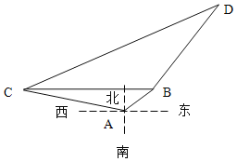
    （1）问船与船相距多少海里？船在船的什么方向？

    （2）问缉私艇沿什么方向行驶才能最快追上走私船？并求出所需时间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1=2，an+1=2（Sn+n+1）（n∈N*），令bn=an+1．

    （1）求数列{bn}的通项公式；

    （2）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司生产某种产品进行出售，当这种产品定价为每吨1000元时，每月可售出产品100吨.当每吨价格每增加20元时，月售出量将会减少1吨.产品每吨生产成本400元，月固定成本为20000元.

    （Ⅰ）当产品每吨定价为1200元时，该公司月利润是多少？

    （Ⅱ）当产品每吨定价为多少元时，该公司的月利润最大？最大月利润是多少？（利润=总收入-生产成本-固定成本）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某超市一年中各月份的收入与支出单位：万元情况的条形统计图已知利润为收入与支出的差，即利润收入一支出，则下列说法正确的是　　

    A. 利润最高的月份是2月份，且2月份的利润为40万元

    B. 利润最低的月份是5月份，且5月份的利润为10万元

    C. 收入最少的月份的利润也最少

    D. 收入最少的月份的支出也最少

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （1）若曲线在点处与直线相切，求的值；

    （2）若函数有两个零点，，试判断的符号，并证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，在圆E上，过点的直线l与圆E相切．

    Ⅰ求圆E的方程；

    Ⅱ求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，网格纸上小正方形的边长为1，粗实线和虚线画出的是某几何体的三视图，则该几何休的表面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一个缆车示意图，该缆车的半径为4.8 m，圆上最低点与地面的距离为0.8 m，缆车每60 s转动一圈，图中OA与地面垂直，以OA为始边，逆时针转动θ角到OB，设B点与地面的距离为h m．

    （1）求h与θ之间的函数解析式；

    （2）设从OA开始转动，经过t s达到OB，求h与t之间的函数解析式，并计算经过45 s后缆车距离地面的高度．

    查看答案和解析>>

    同步练习册答案