
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘缉私艇奉命以
处有一艘缉私艇奉命以![]() 海里/时的速度追截走私船,此时,走私船正以
海里/时的速度追截走私船,此时,走私船正以![]() 海里/时的速度从
海里/时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.
方向逃窜.
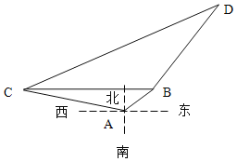
(1)问![]() 船与
船与![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列说法:
①数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的一个通项公式是
…的一个通项公式是![]() ;
;
②当![]() 时,不等式
时,不等式![]() 对一切实数x都成立;
对一切实数x都成立;
③函数![]() 是周期为
是周期为![]() 的奇函数;
的奇函数;
④两两相交且不过同一点的三条直线必在同一个平面内.
其中,正确说法序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|x|≤2,|y|≤2,点P的坐标为(x,y).
(1)求当x,y∈R时,P满足(x-2)2+(y-2)2≤4的概率.
(2)求当x,y∈Z时,P满足(x-2)2+(y-2)2≤4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:

计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点
到焦点![]() 的距离为3 ,直线
的距离为3 ,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点。
为坐标原点。
(1)求抛物线![]() 的方程;
的方程;
(2)求![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与
与![]() 相交于A,B两点,
相交于A,B两点,![]() 的周长为
的周长为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 为直角,若存在求出此时直线
为直角,若存在求出此时直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】钓鱼岛及其附属岛屿是中国固有领土,如图:点A、B、C分别表示钓鱼岛、南小岛、黄尾屿,点C在点A的北偏东47°方向,点B在点C的南偏西36°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为3海里.

(1)求A、C两点间的距离;(精确到0.01)
(2)某一时刻,我国一渔船在A点处因故障抛锚发出求救信号.一艘R国舰艇正从点C正东10海里的点P处以18海里/小时的速度接近渔船,其航线为P![]() C
C![]() A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com