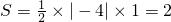已知函数f(x)=aln(x+1)+(x+1)2在x=1处有极值.
(1)求实数a值;
(2)求函数f(x)的单调区间;
(3)令g(x)=f′(x),若曲线g(x)在(1,g(1))处的切线与两坐标轴分别交于A,B两点(O为坐标原点),求△AOB的面积.
解:(Ⅰ)因为f(x)=aln(x+1)+(x+1)
2,
所以
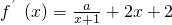
.
由f′(1)=0,可得
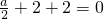
,a=-8.
经检验a=-8时,函数f(x)在x=1处取得极值,
所以a=-8.
(Ⅱ)f(x)=-8ln(x+1)+(x+1)
2,
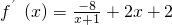
=

.
而函数f(x)的定义域为(-1,+∞),
当x变化时,f′(x),f(x)的变化情况如下表:

由表可知,f(x)的单调减区间为(-1,1),f(x)的单调增区间为(1,+∞).(10分)
(Ⅲ)由于
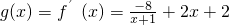
,
所以
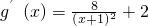
,当x=1时,g′(1)=4,g(1)=0.
所以切线斜率为4,切点为(1,0),
所以切线方程为y=4(x-1),即4x-y-4=0.
令x=0,得y=-4,令y=0,得x=1.
所以△AOB的面积
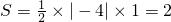
分析:(1)先对f(x)求导,由题意可得,f′(1)=0,代入求a
(2)求函数f(x)的定义域,令f′(x)>0,f′(x)<0分别解出函数的单调增区间、减区间
(3)求g(1)=f′(1)及g′(x),然后求切线的斜率k=g′(1),写出切线方程,求出A,B,进一步求结果.
点评:本题考查了导数的应用:极值在x
0存在的性质,f(x
0)=0;求函数的单调区间:即解f′(x)>0,f′(x)<0;导数的几何意义:函数在x
0处的导数f(x
0)为该点的切线斜率.属于基础知识的综合运用.

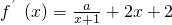 .
.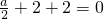 ,a=-8.
,a=-8.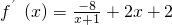 =
= .
.
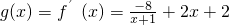 ,
,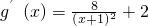 ,当x=1时,g′(1)=4,g(1)=0.
,当x=1时,g′(1)=4,g(1)=0.