
分析 考虑由于正方体绕其体对角线旋转120°后仍与自身重合,于是f(r)在正方体的侧面ABB1A1与BCC1B1上的轨迹长度之和的3倍,对r讨论,(1)当0<r≤1时,(2)当1<r<$\sqrt{2}$时,(3)当$\sqrt{2}$≤r<$\sqrt{3}$时,运用弧长公式,求导数,判断单调性,画出f(r)的大致图象,即可得到方程的所有可能解的个数.
解答 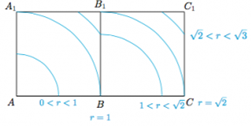 解:由于正方体绕其体对角线旋转120°后仍与自身重合,
解:由于正方体绕其体对角线旋转120°后仍与自身重合,
于是f(r)在正方体的侧面ABB1A1与BCC1B1上的轨迹长度之和的3倍.将右侧面BCC1B1翻折至于侧面ABB1A1重合(如图),
稍加探索发现r=1,r=$\sqrt{2}$是两个分界点.
(1)当0<r≤1时,f(r)=$\frac{3πr}{2}$,于是f($\frac{1}{2}$)=$\frac{3π}{4}$;
(2)当1<r<$\sqrt{2}$时,设圆心角θ=arccos$\frac{1}{r}$,其中θ∈(0,$\frac{π}{4}$),
弧长之和为h(θ)=($\frac{π}{2}$-2θ)•$\frac{1}{cosθ}$+$\frac{π}{2}$•tanθ=$\frac{π}{2}$•$\frac{sinθ-\frac{4θ}{π}+1}{cosθ}$,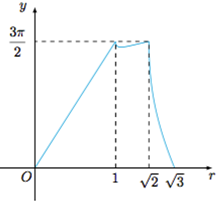
于是h′(θ)=$\frac{π}{2}$•$\frac{1+sinθ-\frac{4}{π}(cosθ+θ•sinθ)}{co{s}^{2}θ}$,
设φ(θ)=1+sinθ-$\frac{4}{π}$(cosθ+θ•sinθ),
则φ(0)=1-$\frac{4}{π}$<0,φ($\frac{π}{4}$)=1-$\frac{4}{π}$•$\frac{\sqrt{2}}{2}$>0,
而φ′(θ)=cosθ(1-$\frac{4}{π}$•θ)>0,
则φ(θ)在(0,$\frac{π}{4}$)上先负后正,对应的h(θ)在(0,$\frac{π}{4}$)先递减后递增;
(3)当$\sqrt{2}$≤r<$\sqrt{3}$时,图中弧长的半径为$\sqrt{{r}^{2}-1}$,
所对的圆心角为$\frac{π}{2}$-2arccos$\frac{1}{\sqrt{{r}^{2}-1}}$,
记θ=arccos$\frac{1}{\sqrt{{r}^{2}-1}}$,其中θ∈[0,$\frac{π}{4}$),则对应的弧长l(θ)=($\frac{π}{2}$-2θ)•$\frac{1}{cosθ}$,
则l′(θ)=$\frac{-2-2θtanθ+\frac{π}{2}tanθ}{cosθ}$<0,于是随r递增,θ递增,对应的弧长递减,即f(r)递减.
这样我们勾勒出函数f(r)的图象,
于是f(r)=k的解的个数所有可能的值为0,2,3,4.
点评 本题考查方程解的个数问题的解法,考查分类讨论思想方法,以及数形结合的思想,注意运用单调性画出f(r)的图象是解题的关键,属于难题.


科目:高中数学 来源: 题型:填空题
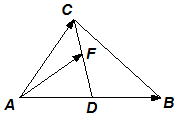 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84π | B. | 96π | C. | 112π | D. | 144π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
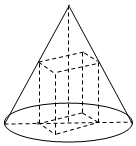 底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
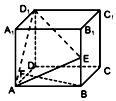 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )| A. | 平行 | B. | 相交但不垂直 | C. | 垂直 | D. | 异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com