
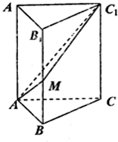
 如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.
如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$. 分析 先将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,
由此可以求得△AMC1的三边长,再由余弦定理求出其中一角,由面积公式求出面积
解答 解:将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1,与BB1的交点即为满足AM+MC1最小时的点M,
由于AB=1,BC=2,AA1=3,再结合棱柱的性质,可得BM=$\frac{1}{3}$AA1=1,故B1M=2
由图形及棱柱的性质,可得AM=$\sqrt{2}$,AC1=$\sqrt{14}$,MC1=2$\sqrt{2}$,cos∠AMC1=$\frac{2+8-14}{2×\sqrt{2}×2\sqrt{2}}$=-$\frac{1}{2}$.
故sin∠AMC1=$\frac{\sqrt{3}}{2}$,△AMC1的面积为$\frac{1}{2}×\sqrt{2}×2\sqrt{2}×\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
设点C到平面AMC1的距离为h,则由等体积可得$\frac{1}{3}×\frac{1}{2}×3×2×1=\frac{1}{3}×\sqrt{3}×h$,
∴h=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查棱柱的特征,求解本题的关键是根据棱柱的结构特征及其棱长等求出三角形的边长,再由面积公式求面积,本题代数与几何相结合,综合性强,解题时要注意运算准确,正确认识图形中的位置关系.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列命题正确的是①②④.(写出所有正确的命题的编号)
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列命题正确的是①②④.(写出所有正确的命题的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,n∥α,则m⊥n | B. | 若m⊥α,n∥m,n?β,则α⊥β | ||
| C. | 若m⊥α,n⊥β,α∥β,则m∥n | D. | 若m∥α,m∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com