
分析 首先分析等式$\frac{f(x)}{x}$=lnx•f′(x),构造g(x)=$\frac{f(x)}{lnx}$,求导发现g(x)为常数函数,因此得到f(x)的解析式,然后判断xf(x)的单调性,从而得到所求.
解答 解:设g(x)=$\frac{f(x)}{lnx}$,则g'(x)=$\frac{f'(x)lnx-\frac{f(x)}{x}}{(lnx)^{2}}$,因为$\frac{f(x)}{x}$=lnx•f′(x),所以g'(x)=0,所以g(x)=c,又f(e)=2,所以g(e)=2,所以g(x)=2,所以f(x)=2lnx,
所以不等式xf(x)<2e为xlnx<elne,
又x>1时,(xlnx)'=lnx+1>0,所以函数y=xlnx为增函数,所以1<x<e,
不等式xf(x)<2e的解集为(1,e);
故答案为:(1,e).
点评 本题考查了构造法求函数的解析式,以及利用导数判定函数的单调性;属于难题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:解答题
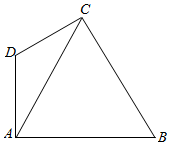 滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12$\sqrt{6}$m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.
滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12$\sqrt{6}$m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{6}{5}$ | B. | -1 | C. | 0 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com