
| Y X | y1 | y2 | 总计 |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A. | a=5,b=4,c=3,d=2 | B. | a=5,b=3,c=4,d=2 | C. | a=2,b=3,c=4,d=5 | D. | a=3,b=2,c=4,d=5 |
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.| 分组 | 频数 |
| [2,4) | 2 |
| [4,6) | 10 |
| [6,8) | 16 |
| [8,10) | 8 |
| [10,12] | 4 |
| 合计 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
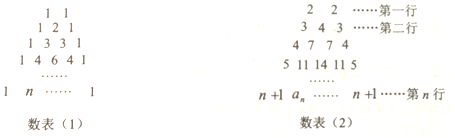
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|0≤x<2} | C. | {x|x<2} | D. | {x|x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 4 | 3 | 2 | 4 | 2 |
| A. | 0.70 | B. | 0.60 | C. | 0.45 | D. | 0.35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com