
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为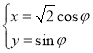 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上一点,此时参数
上一点,此时参数![]() ,将射线
,将射线![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 交曲线
交曲线![]() 于点
于点![]() ,记曲线
,记曲线![]() 的上顶点为点
的上顶点为点![]() ,求
,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
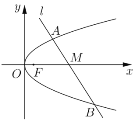
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 轴正半轴上点
轴正半轴上点![]() 的直线
的直线![]() 交
交![]() 于不同的两点
于不同的两点![]() 和
和![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,求证:原点
,求证:原点![]() 总在以线段
总在以线段![]() 为直径的圆的内部;
为直径的圆的内部;
(3)若![]() ,且直线
,且直线![]() ∥
∥![]() ,
,![]() 与
与![]() 有且只有一个公共点
有且只有一个公共点![]() ,问:△
,问:△![]() 的面积是否存在最小值?若存在,求出最小值,并求出
的面积是否存在最小值?若存在,求出最小值,并求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省普通高中学业水平考试成绩按人数所占比例依次由高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,
五个等级,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() 等级
等级![]() ,
,![]() ,
,![]() 等级共
等级共![]() .其中
.其中![]() 等级为不合格,原则上比例不超过
等级为不合格,原则上比例不超过![]() .该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到
.该省某校高二年级学生都参加学业水平考试,先从中随机抽取了部分学生的考试成绩进行统计,统计结果如图所示.若该校高二年级共有1000名学生,则估计该年级拿到![]() 级及以上级别的学生人数有( )
级及以上级别的学生人数有( )
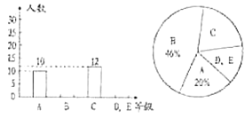
A.45人B.660人C.880人D.900人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,向量![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的范围.
,求a+c的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架“歼-15”舰载机准备着舰,已知乙机不能最先着舰,丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求曲线![]() 在
在![]() 处的切线的方程;
处的切线的方程;
(2)若对于任意实数![]() ,
,![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com