
分析 利用对称点的特点,建立方程组,即可得出结论.
解答 解:设要求的对称点坐标为A′(a,b),则$\left\{\begin{array}{l}{\frac{y-b}{x-a}=1}\\{\frac{x+a}{2}+\frac{y+b}{2}+c=0}\end{array}\right.$
∴a=-y-c,b=-x-c,
∴A′(-y-c,-x-c),
同理关于直线x-y+c=0的对称点A″的坐标为(y-c,x+c),
曲线f(x,y)=0关于直线x+y+c=0的对称曲线为f(-y-c,-x-c)=0,关于直线x-y+c=0的对称曲线为f(y-c,x+c)=0,
故答案为:(-y-c,-x-c);(y-c,x+c);f(-y-c,-x-c)=0;f(y-c,x+c)=0.
点评 本题考查点关于直线的对称点的求法,考查学生的计算能力,正确运用对称点的特点是关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 直角或钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
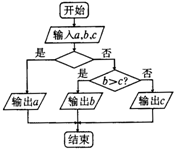
| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
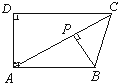 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )| A. | AB与AD | B. | AB与BC | C. | BD与BC | D. | AD与AP |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com