练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】四棱锥中，底面是的菱形，侧面为正三角形，其所在平面垂直于底面.

    （1）若为线段的中点，求证：平面；

    （2）若为边的中点，能否在棱上找到一点，使平面平面？并证明你的结论.

    【答案】（见解析；（2）见解析．

    【解析】分析：（1）取的中点，利用等腰三角形的“三线合一”得到线线垂直，进而利用线面垂直的判定定理进行证明；（2）先利用面面垂直的性质得到线面垂直，进而得到面面垂直，再利用面面垂直的性质得到线线垂直，利用平行四边形确定点的位置．

    详解：（1）如图，取中点，连接，，，

    ∵ 为等边三角形，∴ ，

    在中，，，

    ∴ 为等边三角形，∴ ，

    ∴ 平面.

    （2）连接与相交于点，

    在中，作，交于点，

    ∵ 平面平面，∴ 平面，

    ∴ 平面，

    ∴ 平面平面，

    易知四边形为平行四边形，

    ∴ 是的中点，∴ 是的中点，

    ∴ 在上存在一点，即为的中点，使得平面平面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的右焦点为， 为直线上一点，线段交于点，若，则__________．

    【答案】

    【解析】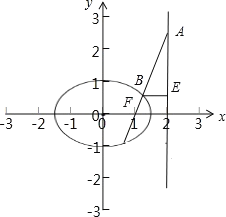

    由条件椭圆： ∴

    椭圆的右焦点为F,可知F(1,0)，

    设点A的坐标为（2，m），则=（1，m），

    ∴，

    ∴点B的坐标为，

    ∵点B在椭圆C上，

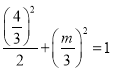    ∴，解得：m=1，

    ∴点A的坐标为（2，1），.

    答案为： .

    【题型】填空题
    【结束】
    16

    【题目】四棱锥中， 面， 是平行四边形， ， ，点为棱的中点，点在棱上，且，平面与交于点，则异面直线与所成角的正切值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （＞b＞0）的左、右顶点分别为A1、A2，上、下顶点分别为B2、B1，O为坐标原点，四边形A1B1A2B2的面积为4，且该四边形内切圆的方程为．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若M、N是椭圆C上的两个不同的动点，直线OM、ON的斜率之积等于，试探求△OMN的面积是否为定值，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    （1）证明函数f ( x )的图象关于轴对称；

    （2）判断在上的单调性，并用定义加以证明；

    （3）当x∈［1，2］时函数f (x )的最大值为，求此时a的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A、B、C所对的边长分别为a、b、c，且acos B＝3，bsin A＝4.

    (1)求边长a；

    (2)若△ABC的面积S＝10，求△ABC的周长l.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中，和是边长为的等边三角形，，分别是的中点．

    （Ⅰ）求证：∥平面；

    （Ⅱ）求证：平面⊥平面；

    （Ⅲ）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】辽宁号航母纪念章从2012年10月5日起开始上市，通过市场调查，得到该纪念章每枚的市场价（单位：元）与上市时间（单位：天）的数据如下：

    上市时间天

    市场价元

    （1）根据上表数据，从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价与上市时间的变化关系：①；②；③；

    （2）利用你选取的函数，求辽宁号航母纪念章市场价最低时的上市天数及最低的价格；

    （3）设你选取的函数为，若对任意实数，关于的方程恒有个想异实数根，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校高一数学考试后，对分(含分)以上的成绩进行统计，其频率分布直方图如图所示，分数在分的学生人数为人，

    （1）求这所学校分数在分的学生人数；

    （2）请根据频率发布直方图估计这所学校学生分数在分的学生的平均成绩；

    （3）为进“步了解学生的学习情况，按分层抽样方法从分数在分和分的学生中抽出人，从抽出的学生中选出人分别做问卷和问卷，求分的学生做问卷，分的学生做问卷的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段，，，，，进行分组.已知测试分数均为整数，现用每组区间的中点值代替该组中的每个数据，则得到体育成绩的折线图如下：

    （1）若体育成绩大于或等于70分的学生为“体育良好”，已知该校高一年级有1000名学生，试估计该校高一年级学生“体育良好”的人数；

    （2）用样本估计总体的思想，试估计该校高一年级学生达标测试的平均分；

    （3）假设甲、乙、丙三人的体育成绩分别为，且，，，当三人的体育成绩方差最小时，写出的所有可能取值（不要求证明）

    查看答案和解析>>

    同步练习册答案