
分析 (1)根据平面向量共线定理,列出方程,利用三角恒等变换求出角A的值;
(2)由余弦定理和基本不等式求出△ABC面积S的最大值,并判断S取最大值时△ABC是等边三角形.
解答 解:(1)向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$)与向量$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA)共线,
∴sinA•(sinA+$\sqrt{3}$cosA)-$\frac{3}{2}$=0,…2分
∴$\frac{1-cos2A}{2}$+$\frac{\sqrt{3}}{2}$sin2A-$\frac{3}{2}$=0,
即$\frac{\sqrt{3}}{2}$sin2A-$\frac{1}{2}$cos2A=1,
即sin(2A-$\frac{π}{6}$)=1;…4分
又∵A∈(0,π),
∴2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{11π}{6}$),
∴2A-$\frac{π}{6}$=$\frac{π}{2}$,
解得A=$\frac{π}{3}$;…6分
(2)由余弦定理得:16=b2+c2-bc,
∴16+bc=b2+c2≥2bc,
即bc≤16(当且仅当b=c时取等号);
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc≤4$\sqrt{3}$,
∴S的最大值是4$\sqrt{3}$,…9分
当S取最大值时,b=c;
又∵A=$\frac{π}{3}$,
∴△ABC是等边三角形.…12分
点评 本题考查了平面向量的共线定理与正弦、余弦定理的应用问题,是中档题.


科目:高中数学 来源: 题型:选择题
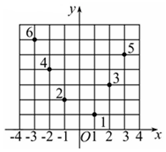 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )| A. | 2 011 | B. | 1 006 | C. | 1 005 | D. | 1 003 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
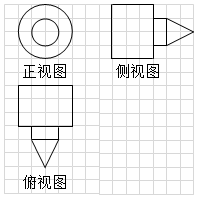 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{5}-\sqrt{3}}}{6}$ | C. | $\frac{{2\sqrt{3}-\sqrt{5}}}{6}$ | D. | $\frac{{4-\sqrt{15}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com