
| x |
| 1+x |
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 20 | 80 |
| 北方学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
| P(x2>k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多可运行台数 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
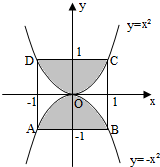 正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是
正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com