
【题目】设![]() 为给定的大于2的正整数,集合
为给定的大于2的正整数,集合![]() ,已知数列
,已知数列![]() :
:![]() ,
,![]() ,…,
,…,![]() 满足条件:
满足条件:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() .
.
如果对于![]() ,有
,有![]() ,则称
,则称![]() 为数列
为数列![]() 的一个逆序对.记数列
的一个逆序对.记数列![]() 的所有逆序对的个数为
的所有逆序对的个数为![]() .
.
(1)若![]() ,写出所有可能的数列
,写出所有可能的数列![]() ;
;
(2)若![]() ,求数列
,求数列![]() 的个数;
的个数;
(3)对于满足条件的一切数列![]() ,求所有
,求所有![]() 的算术平均值.
的算术平均值.
【答案】(1)不同的![]() 分别为:
分别为:![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据![]() 可列出满足条件的
可列出满足条件的![]() .
.
(2)就构成逆序对的元素的个数分类计数可得满足条件的![]() 的个数.
的个数.
(3)引进一个定义:![]() ,有
,有![]() ,则称
,则称![]() 为数列
为数列![]() 的一个顺序对,可证明所有的
的一个顺序对,可证明所有的![]() 中,逆序对的总数和顺序对的总数相等,从而可得逆序对的个数为
中,逆序对的总数和顺序对的总数相等,从而可得逆序对的个数为![]() ,故可求其平均值.
,故可求其平均值.
(1)因为![]() , 故
, 故![]() 只有一个逆序对,
只有一个逆序对,
则不同的![]() 分别为:
分别为:![]() .
.
(2)因为![]() ,故数列
,故数列![]() :
:![]() ,
,![]() ,…,
,…,![]() 有两种情况:
有两种情况:
①2对逆序数由3个元素提供,即
![]() ,
,
这样的![]() 共有
共有![]() 个.
个.
②2对逆序数由4个元素提供,即
![]() .
.
这样的![]() 共有
共有![]() .
.
综上,满足![]() 的数列
的数列![]() 的个数为
的个数为![]() .
.
(3)对任意的![]() :
:![]() ,
,![]() ,…,
,…,![]() ,其逆序对的个数为
,其逆序对的个数为![]() ,
,
我们引进一个定义:![]() ,有
,有![]() ,则称
,则称![]() 为数列
为数列![]() 的一个顺序对,
的一个顺序对,
则![]() 中的顺序对个数为
中的顺序对个数为![]() .
.
考虑![]() :
:![]() ,
,![]() ,…,
,…,![]() 与
与![]() :
:![]() ,
,![]() ,…,
,…,![]() ,
,
![]() 中的逆序对的个数为
中的逆序对的个数为![]() 中顺序对的个数,
中顺序对的个数,![]() 中顺序对的个数为
中顺序对的个数为![]() 中逆序对个数,
中逆序对个数,
把所有的![]() 按如上形式两两分类,则可得所有的
按如上形式两两分类,则可得所有的![]() 中,逆序对的总数和顺序对的总数相等,而它们的和为
中,逆序对的总数和顺序对的总数相等,而它们的和为![]() ,故逆序对的个数为
,故逆序对的个数为![]() ,
,
所以所有![]() 的算术平均值为
的算术平均值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.


![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为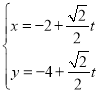 (t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)已知定点![]() ,直线
,直线![]() 与曲线C分别交于P、Q两点,求
与曲线C分别交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以昆明、玉溪为中心的滇中地区,冬无严寒、夏无酷暑,世界上主要的鲜切花品种在这里都能实现周年规模化生产.某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰,由于库房限制每天最多加工6箱.
(1)若某天该鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,则恰好一位是以2000元价格购买的顾客,另一位是以1200元价格购买的顾客的概率是多少?
(2)该鲜花批发店统计了100天内该种玫瑰在每天下午3点以前的销售量![]() (单位:箱),统计结果如下表所示(视频率为概率):
(单位:箱),统计结果如下表所示(视频率为概率):
| 4 | 5 | 6 |
频数 | 30 |
|
|
①估计接下来的一个月(30天)内该种玫瑰每天下午3点以前的销售量不少于5箱的天数是多少?
②若批发店每天在购进5箱数量的玫瑰时所获得的平均利润最大(不考虑其他成本),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率
的左、右焦点,离心率![]() ,过椭圆
,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(Ⅲ)设点![]() 是一个动点,若直线
是一个动点,若直线![]() 的斜率存在,且
的斜率存在,且![]() 为
为![]() 中点,
中点,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
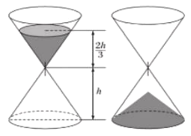
【题目】沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).假设该沙漏每秒钟漏下
(细管长度忽略不计).假设该沙漏每秒钟漏下![]() 的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
A.沙漏中的细沙体积为![]()
B.沙漏的体积是![]()
C.细沙全部漏入下部后此锥形沙堆的高度约为2.4cm
D.该沙漏的一个沙时大约是1985秒(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com