Question

15．设函数f（x）=a²x²（a＞0），$g（x）=\sqrt{9-{{（x-b）}^2}}$．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为$\sqrt{2}$，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设$a=\frac{{\sqrt{2}}}{2}$，$b=\frac{{5\sqrt{3}}}{2}$，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

Answer 1

分析 （1）直接运用点到直线的距离公式，然后求解即可得到答案；
（2）关于由不等式解集整数的个数，然后求未知量取值范围的题目，可利用恒等变换，把它转化为求函数零点的问题，即可求得a的范围；
（3）分别画出f（x），g（x）的图象，再令f（x）=g（x），求得交点，求出与y=f（x）相切的直线，检验是否与y=g（x）也相切，即可得到所求分界线．

解答 解：（1）因为f（x）=a²x²，
所以f′（x）=2a²x，令f′（x）=2a²x=1，
得：x=$\frac{1}{2{a}^{2}}$，此时y=$\frac{1}{4{a}^{2}}$，
则点（$\frac{1}{2{a}^{2}}$，$\frac{1}{4{a}^{2}}$）到直线x-y-3=0的距离为$\sqrt{2}$，
即$\frac{|\frac{1}{2{a}^{2}}-\frac{1}{4{a}^{2}}-3|}{\sqrt{2}}$=$\sqrt{2}$，解之得a=$\frac{1}{2}$或$\frac{\sqrt{5}}{10}$；
（2）不等式（x-1）²＞f（x）的解集中的整数恰有3个，
等价于（1-a²）x²-2x+1＞0恰有三个整数解，故1-a²＜0，
令h（x）=（1-a²）x²-2x+1，由h（0）=1＞0且h（1）=-a²＜0（a＞0），
所以函数h（x）=（1-a²）x²-2x+1的一个零点在区间（0，1），
则另一个零点一定在区间（-3，-2），
这是因为此时不等式解集中有-2，-1，0恰好三个整数解．
故$\left\{\begin{array}{l}{h（-2）＞0}\\{h（-3）≤0}\end{array}\right.$，即为$\left\{\begin{array}{l}{4（1-{a}^{2}）+5＞0}\\{9（1-{a}^{2}）+7≤0}\end{array}\right.$，解之得$\frac{4}{3}$≤a＜$\frac{3}{2}$；
（3）分别作出函数f（x）=$\frac{1}{2}$x²，g（x）=$\sqrt{9-（x-\frac{5\sqrt{3}}{2}）^{2}}$的图象，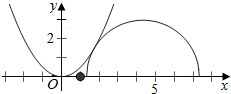
发现它们有一个交点．
令f（x）=g（x），可得$\frac{1}{4}$x⁴+（x-$\frac{5\sqrt{3}}{2}$）²=9，
解得x=$\sqrt{3}$，交点为（$\sqrt{3}$，$\frac{3}{2}$），
可设与y=f（x）相切的直线l方程为y-$\frac{3}{2}$=k（x-$\sqrt{3}$），
由f（x）的导数f′（x）=x，
可得切线的斜率为k=$\sqrt{3}$，
则切线l的方程为$\sqrt{3}$x-y-$\frac{3}{2}$=0，
又g（x）的图象是（$\frac{5}{2}$$\sqrt{3}$，0）为圆心，3为半径的上半圆．
由圆心到直线l的距离为d=$\frac{|\sqrt{3}•\frac{5\sqrt{3}}{2}-\frac{3}{2}|}{\sqrt{3+1}}$=3，
则直线l也与y=g（x）的图象相切．
则直线y=$\sqrt{3}$x-$\frac{3}{2}$即为f（x）、g（x）的分界线．

点评 此题主要考查点到直线距离公式的应用及不等式的解法，此类型的题目需要仔细分析再求解，综合性较强，有一定的技巧性．