
分析 (1)利用对数性质、运算法则求解.
(2)利用对数性质、运算法则求解.
解答 解:(1)${log_2}\sqrt{\frac{7}{72}}+{log_2}6-\frac{1}{2}{log_2}28$
=${log}_{2}(\sqrt{\frac{7}{72}}×6÷\sqrt{28})$
=$lo{g}_{2}\sqrt{\frac{1}{8}}$
=$lo{g}_{2}{2}^{-\frac{3}{2}}$
=-$\frac{3}{2}$.
(2)log${\;}_{\sqrt{2}}$2+log927+$\frac{1}{4}$log4$\frac{1}{16}$+2${\;}^{1+lo{g}_{2}9}$
=2+$\frac{3}{2}$-$\frac{1}{2}$+18
=21.
点评 本题考查对数式化简求值,是基础题,解题时要认真审题,注意对数性质、运算法则的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
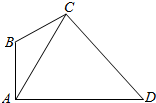 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25人 | B. | 15 人 | C. | 30 人 | D. | 20人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
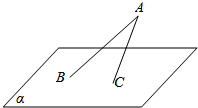 如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.
如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com