
| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
分析 由椭圆可知,对任意实数x,ax2-ax+1>0恒成立,然后分a=0和a≠0讨论,当a≠0时,利用二次函数的开口方向和判别式求解.
解答 解:∵函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,
∴对任意实数x,ax2-ax+1>0恒成立,
当a=0时,满足题意;
当a≠0时,需$\left\{\begin{array}{l}{a>0}\\{(-a)^{2}-4a<0}\end{array}\right.$,即0<a<4.
综上,a的取值范围是[0,4).
故选:D.
点评 本题考查函数的定义域及其求法,考查了恒成立问题,体现了分类讨论的数学思想方法,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
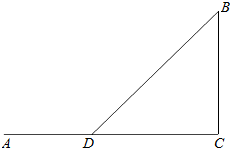 如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.
如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com