
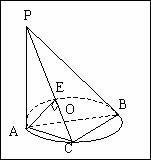
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是异于A、B的⊙O上任意一点,过A作AE⊥PC于E ,
求证:(1)BC⊥平面PAC(2)AE⊥平面PBC
科目:高中数学 来源: 题型:
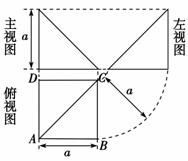
四棱锥PABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,根据图中的信息,在四棱锥的任两个顶点的连线中,互相垂直的异面直线对数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线与平面所成的角
(1)一个平面的斜线和它在这个平面内的)______所成的角,叫做斜线和这个平面所成的角.
(2)直线与平面所成的角的范围是_________
(3)如果直线和平面垂直,那么就说直线和平面所成的角是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
在如图所示的几何体中,四边形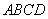 是菱形,
是菱形, 是矩形,平面
是矩形,平面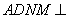 平面
平面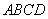 ,
, 为
为 的中点.
的中点.
(1)求证: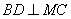 ;
;
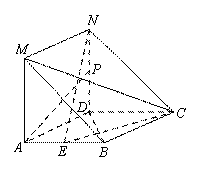
(2)在线段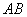 上是否存在点
上是否存在点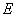 ,使得
,使得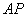 ∥平面
∥平面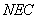 ,
,
若存在,说明其位置,并加以证明;若不存在,请说明理由.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某高速公路收费站入口处的安全标识墩如图4所示.墩的上半部分是正四棱锥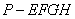 ,下半部分是长方体
,下半部分是长方体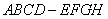 .图5、图6分别是该标识墩的正(主)视图和俯视图.(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;(3)证明:直线
.图5、图6分别是该标识墩的正(主)视图和俯视图.(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;(3)证明:直线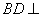 平面
平面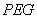 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
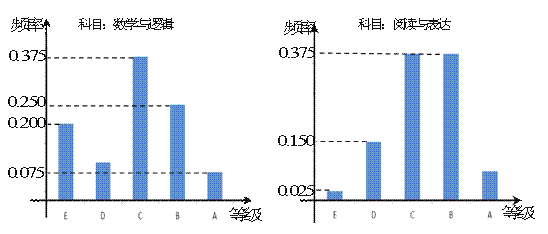
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求 该考场考生“数学与逻辑”科目的平均分;
该考场考生“数学与逻辑”科目的平均分; 
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访 谈,求这两人的两科成绩均为A的概率.
谈,求这两人的两科成绩均为A的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com