
分析 (I)Sn=$\frac{3}{2}$(an-1),可得n≥2时,an=Sn-Sn-1,化为:an=3an-1.n=1时,a1=$\frac{3}{2}({a}_{1}-1)$,解得a1.利用等比数列的通项公式可得an.b6=a3=33=27,b60=a5=35.数列{bn}满足bn+2=2bn+1-bn,即bn+2+bn=2bn+1,利用等差数列通项公式即可得出.
(II)cn=(-1)nbnbn+1=(-1)n(4n+3)(4n+7).计算c2k-1+c2k,对n分类讨论即可得出.
解答 解:(I)∵Sn=$\frac{3}{2}$(an-1),∴n≥2时,an=Sn-Sn-1=$\frac{3}{2}$(an-1)-$\frac{3}{2}({a}_{n-1}-1)$,化为:an=3an-1.
n=1时,a1=$\frac{3}{2}({a}_{1}-1)$,解得a1=3.
∴数列{an}是等比数列,首项与公比都为3.
∴an=3n.
b6=a3=33=27,b60=a5=35.
数列{bn}满足bn+2=2bn+1-bn,即bn+2+bn=2bn+1,
∴数列{bn}是等差数列,设公差为d,则b1+5d=27,b1+59d=243.
联立解得b1=7,d=4.
∴bn=7+4(n-1)=4n+3.
(II)cn=(-1)nbnbn+1=(-1)n(4n+3)(4n+7).
c2k-1+c2k=-(8k-1)(8k+3)+(8k+3)(8k+7)=48k+18.
∴n=2k(k∈N*)时,数列{cn}的前n项和Tn=T2k=(c1+c2)+(c3+c4)+…+(c2k-1+c2k)
=48×(1+2…+k)+18k=$48×\frac{k(1+k)}{2}$+18k=24k2+42k=6n2+21n.
n=2k-1时,T2k-1=T2k-2+c2k-1=6(n-1)2+21(n-1)-(8k-1)(8k+3)=6(n-1)2+21(n-1)-(4n+3)(4n+7)=-10n2-31n-36.
∴Tn=$\left\{\begin{array}{l}{6{n}^{2}+21n,n为偶数}\\{-10{n}^{2}-31n-36,n为奇数}\end{array}\right.$.
点评 本题考查了等差数列与等比数列的通项公式求和公式、分类讨论方法、数列递推关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${x^2}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{5}=1$ | D. | ${x^2}-\frac{y^2}{6}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
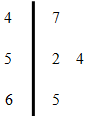 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
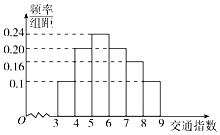 随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com