练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知sinx+cosy=$\frac{3}{5}$，则μ=sinx-cos2y的最大值为$\frac{21}{25}$．

    分析 角三角函数的基本关系、余弦函数的值域、二次函数的性质，求得μ的最大值．

    解答 解：∵sinx+cosy=$\frac{3}{5}$，∴cosy=sinx+$\frac{3}{5}$∈[-$\frac{2}{5}$，1]，则μ=sinx-cos2y=$\frac{3}{5}$-cosy-cos2y=-${（cosy+\frac{1}{2}）}^{2}$+$\frac{17}{20}$，
    再根据cosy∈[-$\frac{2}{5}$，1]，可得当cosy=-$\frac{2}{5}$时，函数μ取得最大值为$\frac{84}{100}$=$\frac{21}{25}$，
    故答案为：$\frac{21}{25}$．

    点评 本题主要考查同角三角函数的基本关系、余弦函数的值域、二次函数的性质应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

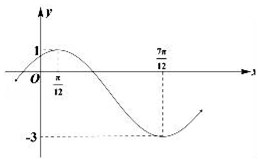    1．已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示：
    （1）求f（x）的解析式；
    （2）求f（x）对称中心坐标和对称轴方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数$y=sin（{2x-\frac{π}{3}}）$在$[{-\frac{π}{2}，\frac{π}{2}}]$上的单调递增区间为[-$\frac{π}{12}$，$\frac{5π}{12}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，4）．
    （1）求$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角；
    （2）若$\overrightarrow{c}$满足$\overrightarrow{c}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），（$\overrightarrow{c}$+$\overrightarrow{a}$）∥$\overrightarrow{b}$，求$\overrightarrow{c}$的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知正项数列{an}满足2an+1=an+an+2，且S2n-1=an2，其中Sn为数列{an}的前n项和，若实数λ使得不等式$\frac{（n+8）{a}_{n}+70}{λ}$≥n恒成立，则实数λ的最大值为$\frac{112}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．不等式|x-1|-|x+1|≥a有解，则a的取值范围为（-∞，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设{an}是首项为3的正项数列，且（n+1）an+12-nan2+an+1•an=0（n=1，2，3，…），则它的通项公式an=$\frac{3}{n}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．角-1540°为第三象限角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，已知圆锥OO1和圆柱O1O2的组合体（它们的底面重合），圆锥的底面圆O1半径为r=5，OA为圆锥的母线，AB为圆柱O1O2的母线，D、E为下底面圆O2上的两点，且DE=6，AB=6.4，AO=5$\sqrt{2}$，AO⊥AD．
    （1）求证：平面ABD⊥平面ODE；
    （2）求二面角B-AD-O的正弦值．

    查看答案和解析>>

    同步练习册答案