
【题目】设函数![]() .
.
(Ⅰ)证明:当![]() 时,
时,![]() ;
;
(Ⅱ)设当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
试题(Ⅰ)在证明不等式时一般可以通过等价变形将要证明的不等式简化,本题中注意到![]() 时,
时,![]() ,于是有
,于是有![]() ,即
,即![]() 令
令![]() 只需证明
只需证明![]() 即可;(Ⅱ)由
即可;(Ⅱ)由![]() 时,
时,![]() 恒成立,故
恒成立,故![]() .
.
设![]() ,
,![]() ,
,![]()
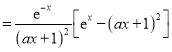 .
.
设![]() ,
,![]() ,则
,则![]() .
.![]() 当
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() ,故
,故![]() .所以
.所以![]() 单调递增,
单调递增,![]() ,故
,故![]() 单调递增,
单调递增,![]() 恒成立,符合题意.当
恒成立,符合题意.当![]() ,即
,即![]() 时,存在
时,存在![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,与
,与![]() 恒成立矛盾.
恒成立矛盾.
试题解析:(Ⅰ)证明:注意到![]() 时,
时,![]() ,
,
于是有![]() ,即
,即![]() .
.
令![]() ,
,![]() .
.![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
可见![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,
![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() ,从而
,从而![]() ,且当且仅当
,且当且仅当![]() 时等号成立.
时等号成立.
(Ⅱ)解:由![]() 时,
时,![]() 恒成立,故
恒成立,故![]() .
.
设![]() ,
,![]() ,
,
则![]()
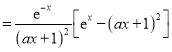 .
.
设![]() ,
,![]() ,
,
则![]() .
.![]()
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() ,故
,故![]() .
.
所以![]() 单调递增,
单调递增,![]() ,故
,故![]() 单调递增,
单调递增,![]() 恒成立,符合题意.
恒成立,符合题意.
当![]() ,即
,即![]() 时,存在
时,存在![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,与
,与![]() 恒成立矛盾.
恒成立矛盾.
综合上述得实数![]() 的取值范围是
的取值范围是![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源: 题型:
【题目】如果函数f(x)=![]() x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
A. [-![]() ,
, ![]() ]
]
B. [-![]() ,
, ![]() ]
]
C. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
D. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据被墨迹污损不清(如图1),但甲得分的折线图完好(如图2),则下列结论错误的是( )
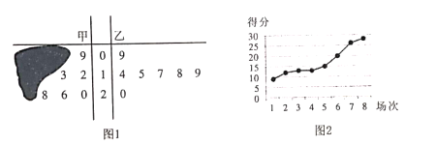
A.乙运动员得分的中位数是17,甲运动员得分的极差是19
B.甲运动员发挥的稳定性比乙运动员发挥的稳定性差
C.甲运动员得分有![]() 的叶集中在茎1上
的叶集中在茎1上
D.甲运动员得分的平均值一定比乙运动员得分的平均值低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线
为抛物线![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和抛物线
和抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() ,试问直线
,试问直线![]() (
(![]() 为抛物线
为抛物线![]() 上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,
,![]() .
.
(1)若集合![]() 含有三个元素,且
含有三个元素,且![]() ,这样的集合
,这样的集合![]() 有多少个?所有集合
有多少个?所有集合![]() 中个元素之和是多少?
中个元素之和是多少?
(2)若集合![]() 各含有三个元素,且
各含有三个元素,且![]() ,
,![]() ,
,![]() ,这样的集合
,这样的集合![]() 有多少种配对方式?
有多少种配对方式?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com