
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)函数
;(2)函数![]() 只有一个零点;(3)
只有一个零点;(3)![]() .
.
【解析】
(1)先求导数![]() ,代入
,代入![]() 得
得![]() 为直线的斜率,利用点斜式可求直线方程;
为直线的斜率,利用点斜式可求直线方程;
(2)先求导数,结合导数的符号,判定零点的个数;
(3)![]() 为增函数,转化为
为增函数,转化为![]() 恒成立,然后利用分离参数法求解.
恒成立,然后利用分离参数法求解.
(1)∵![]() ,∴切线的斜率
,∴切线的斜率![]() ,
,![]() .
.
∴函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 存在零点
存在零点![]() ,且
,且![]() .∵
.∵![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,由
时,由![]() 得
得
![]() .∴
.∴![]() 在
在![]() 上是减函数.
上是减函数.
∴若![]() ,
,![]() ,
,![]() ,则
,则![]() .∴函数
.∴函数![]() 只有一个零点
只有一个零点![]() ,且
,且![]() .
.
(3)解: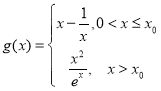 ,故
,故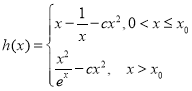 ,
,
∵函数![]() 只有一个零点
只有一个零点![]() ,∴
,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∴![]() 在
在![]() 为增函数
为增函数![]() 在
在![]() ,
,![]() 恒成立.
恒成立.
当![]() 时
时![]() ,即
,即![]() 在区间
在区间![]() 上恒成立.
上恒成立.
设![]() ,只需
,只需![]() ,
,
![]() ,
,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() 的最小值
的最小值![]() ,
,![]() .
.
当![]() 时,
时,![]() ,由上述得
,由上述得![]() ,则
,则![]() 在
在![]() 恒成立.
恒成立.
综上述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
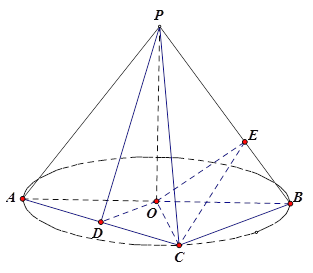
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 体积的最大值;
体积的最大值;
(Ⅲ)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示.
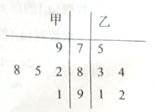
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
,![]() .
.
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计,频率分布直方图如图所示:
(单位:克)中,经统计,频率分布直方图如图所示:
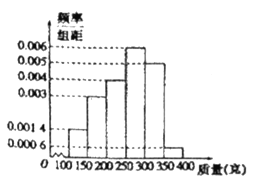
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有1000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com