
| A. | (2,3) | B. | (1,2) | C. | (0,1) | D. | (3,4) |
分析 方法一:在同一平面直角坐标系中,画出函数y=lgx与y=-x+3的图象.它们的交点横坐标x0,显然在区间(1,3)内,由于画图精确性的限制,单凭直观就比较困难了.实际上这是要比较x0与2的大小.当x=2时,lgx=lg2,3-x=1.由于lg2<1,因此x0>2,从而得到答案.
方法二:利用根的存在性定理进行判断即可.
解答 解:方法一:lgx+x-3=0可化为:lgx=-x+3,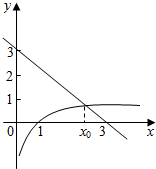
在同一平面直角坐标系中,画出函数y=lgx与y=-x+3的图象.
它们的交点横坐标x0.
当x=2时,lgx=lg2,3-x=1.
∵lg2<1=lg10,
∴x0>2,
从而判定x0∈(2,3).
方法二:因为f(2)=lg2+2-3=lg2-1=lg2-lg10<0,
f(3)=lg3+3-3=lg3>0,
所以根据根的存在性定理可知,函数f(x)在区间(2,3)内存在零点,
所以方程lgx+x-3=的根x0所在的区间为(2,3).
故选:A
点评 本题主要考查了函数的零点与方程根的关系,考查通过构造函数用数形结合法求方程lgx+x-3=0解所在的区间.数形结合,要在结合方面下功夫.不仅要通过图象直观估计,而且还要计算x0的邻近两个函数值,通过比较其大小进行判断.


科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
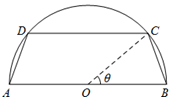 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com