
【题目】在直角坐标系![]() 中,过点
中,过点![]() 作直线
作直线![]() 交
交![]() 轴于A点、交
轴于A点、交![]() 轴于B点,且P位于AB两点之间.
轴于B点,且P位于AB两点之间.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求当![]() 取得最小值时直线
取得最小值时直线![]() 的方程;
的方程;
(3)当![]() 面积最小值时的直线方程.
面积最小值时的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
设直线![]() 可求出
可求出![]() ,
,![]() .结合
.结合![]() 位于
位于![]() 之间,建立关于
之间,建立关于![]() 的不等式,可得
的不等式,可得![]() .
.
(1)由![]() 的坐标,得出向量
的坐标,得出向量![]() 和
和![]() 坐标,从而将
坐标,从而将![]() 化为关于
化为关于![]() 的方程,解出
的方程,解出![]() 值,即得直线
值,即得直线![]() 的方程;
的方程;
(2)由向量数量积的坐标运算公式,得出![]() 关于
关于![]() 的表达式,再用基本不等式得到
的表达式,再用基本不等式得到![]() 取得最小值时
取得最小值时![]() 的斜率
的斜率![]() ,从而得到直线
,从而得到直线![]() 的方程.
的方程.
(3)求出![]() ,再利用基本不等式求最小值,从而得到等号成立的条件,即
,再利用基本不等式求最小值,从而得到等号成立的条件,即![]() ,由此能求出当
,由此能求出当![]() 面积最小值时的直线方程.
面积最小值时的直线方程.
由题意知,直线![]() 的斜率
的斜率![]() 存在且
存在且![]() ,
,
设![]() ,得令
,得令![]() ,得
,得![]() ,所以
,所以![]() ,
,
再令![]() ,得
,得![]() ,所以
,所以![]() ,
,
∵点![]() 位于
位于![]() 两点之间,∴
两点之间,∴![]() 且
且![]() ,解得
,解得![]() .
.
∴![]() ,
,![]() ,
,
(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
∴当![]() 取得最小值时直线
取得最小值时直线![]() 的方程为
的方程为![]() ,
,
化为一般式:![]() .
.
(3)∵![]() ,
,![]() ,
,![]() ,
,
∴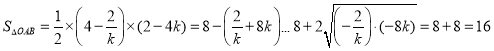 ,
,
当![]() 时,即
时,即![]() 时,取等号,
时,取等号,
∴当![]() 面积最小值时的直线方程为
面积最小值时的直线方程为![]() ,即
,即![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
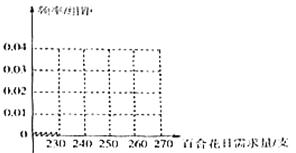
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,
,![]() .如果集合
.如果集合![]() 满足:对于任意的
满足:对于任意的![]() ,都有
,都有![]() ,那么称集合
,那么称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)写出一个具有性质![]() 的集合
的集合![]() ;
;
(Ⅱ)证明:对任意具有性质![]() 的集合
的集合![]() ,
,![]() ;
;
(Ⅲ)求具有性质![]() 的集合
的集合![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查消费者的维权意识,青岛二中的学生记者在五四广场随机调查了120名市民,按他们的年龄分组:第1组[20.30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70),得到的频率分布直方图如图所示.
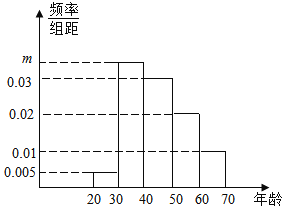
(1)若要从被调查的市民中选1人采访,求被采访人恰好在第2组或第5组的概率;
(2)已知第1组市民中男性有2人,学生要从第1组中随机抽取3名市民组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
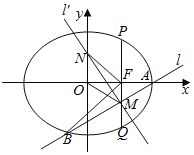
(1)求椭圆的方程;
(2)过点A的直线l与椭圆交于另一点B,垂直于l的直线l′与直线l交于点M,与y轴交于点N,若FB⊥FN且|MO|=|MA|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
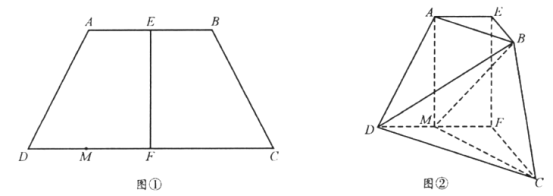
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
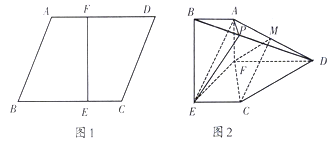
(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com