考点:数列的求和,等差数列的通项公式,等比数列的通项公式,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出{a
n}是首项为a,公比为a的等比数列,由此能求出{a
n}的通项公式.
(Ⅱ)由a=
,得a
n=
()n,
bn =2-(
-
)>2-(
-),由此利用裂项求和法能证明T
n>2n-.
解答:
(Ⅰ)解:∵S
n=
(a
n-1),
∴n=1时,
S1=a1=(a1-1),解得
a1 =a.…(2分)
当n≥2时,有a
n=S
n-S
n-1=
an-an-1,
解得
=a,…(4分)
∴{a
n}是首项为a,公比为a的等比数列.…(5分)
∴
an=a•an-1=an.…(6分)
(Ⅱ)证明:∵a=
,∴a
n=
()n,…(7分)
∴
bn =
+=
+
=
+=1-
+1+
=2-(
-
),…(9分)
由
<,
>,
得
-<-,…(11分)
∴
bn=2-(-)>2-(
-),…(12分)
∴
Tn =b
1+b
2+…+b
n>[2-(
-)]+[2-(
-)]+…+[2-(
-)]
=2n-[(
-)+(
-)+…+(
-)]
=2n-(
-)>2n-
.
即T
n>2n-.…(14分)
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.



 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
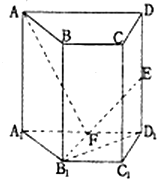 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.

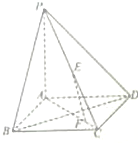 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.