
| A. | e | B. | e2 | C. | e-2 | D. | e-1 |
分析 设出公共点的坐标,求出函数的导数,利用导数的几何意义建立方程关系进行求解即可.
解答 解:y=ln$\sqrt{x}$=$\frac{1}{2}$lnx,
设公共点的坐标为(m,$\frac{1}{2}$lnm),
则函数y=f(x)=a$\sqrt{x}$(a>0)的导数f′(x)=$\frac{a}{2\sqrt{x}}$,
曲线y=g(x)=$\frac{1}{2}$lnx的导数g′(x)=$\frac{1}{2x}$,
则f′(m)=$\frac{a}{2\sqrt{m}}$,g′(m)=$\frac{1}{2m}$,
则由f′(m)=g′(m),得$\frac{a}{2\sqrt{m}}$=$\frac{1}{2m}$,(m>0),
则a=$\frac{1}{\sqrt{m}}$,
又a$\sqrt{m}$=ln$\sqrt{m}$,
即ln$\sqrt{m}$=1,得$\sqrt{m}$=e,则a=$\frac{1}{e}$,
故选:D.
点评 本题主要考查导数的几何意义,求函数的导数,建立方程关系是解决本题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2014}{2015}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
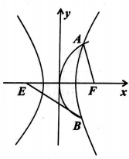 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )| A. | 4-$\sqrt{7}$ | B. | 4-$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 4+$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com