定义在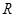
上的函数
同时满足以下条件：①函数
在
上是减函数，在
上是增函数；②
是偶函数；③函数在
处的切线与直线
垂直.
（Ⅰ）求函数的解析式；
（Ⅱ）设
，若存在
使得
，求实数
的取值范围.
黄冈海淀全程培优测试卷系列答案科目：高中数学 来源： 题型：解答题
统计表明，某种型号的汽车在匀速行驶中每小时的耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：
．已知甲、乙两地相距100千米．
（I）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
对于函数
，若在定义域内存在实数
，满足
，则称为“局部奇函数”．
（Ⅰ）已知二次函数
，试判断是否为“局部奇函数”？并说明理由；
（Ⅱ）若
是定义在区间
上的“局部奇函数”，求实数
的取值范围；
（Ⅲ）若
为定义域
上的“局部奇函数”，求实数的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;（Ⅱ）
.（Ⅱ）一般地若存在
使得
，则
;若存在
，则
.在本题中，由
.则
的最小值.
,由题设可得:
即: 
由题意得: 
所以
在
单调递增,在
上单调递减
,所以
对任意
满足
，
，若当
时，
（
且
），且
．
的值；
的值域．
．
，解不等式
；
，
，求实数
的取值范围．
（
）．
的定义域和值域均是
，求实数
的值；
，
，总有
，求实数
，解不等式
；
时，若
，使得不等式
成立，求实数
的取值范围．
的定义域是
，
是
在
的单调区间；
，求
的取值范围；
是
，求证：
.
在点
处的切线方程为
．
，
的值；
定义域内的任一个实数
，
恒成立，求实数
的取值范围．