
【题目】如图,已知抛物线![]() :
: ![]() 与圆
与圆![]() :
: ![]() (
(![]() )相交于
)相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点.
四个点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)当四边形![]() 的面积最大时,求对角线
的面积最大时,求对角线![]() 、
、![]() 的交点
的交点![]() 的坐标.
的坐标.

【答案】(1) (2)
(2)![]()
【解析】(Ⅰ)将抛物线![]() 代入圆
代入圆![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .............(1)
.............(1)
抛物线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴![]()
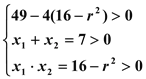 即{
即{
![]() 解这个不等式组得
解这个不等式组得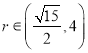 .
.
(II) 设四个交点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() 。则直线AC、BD的方程分别为
。则直线AC、BD的方程分别为
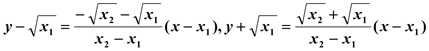
解得点P的坐标为![]() 。则由(I)根据韦达定理有
。则由(I)根据韦达定理有![]() ,
,  由于四边形ABCD为等腰梯形,因而其面积
由于四边形ABCD为等腰梯形,因而其面积![]()
![]()
令![]() ,则
,则![]() 下面求
下面求![]() 的最大值。
的最大值。
方法1:由三次均值有:
![]()
![]()
当且仅当![]() ,即
,即![]() 时取最大值。经检验此时
时取最大值。经检验此时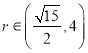 满足题意。故所求的点P的坐标为
满足题意。故所求的点P的坐标为![]()
法2:令![]() ,
,![]() ,
,
∴![]() ,
,
令![]() 得
得![]() ,或
,或![]() (舍去)
(舍去)
当![]() 时,
时,![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时,
时,![]()
故当且仅当![]() 时,
时,![]() 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-1|+|2x-1|.
(Ⅰ)若对![]() x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=2M.证明:a+b≥2ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2cos
=(2cos![]() ,
, ![]() sin
sin![]() ),
),![]() =(cos
=(cos![]() ,2cos
,2cos![]() ),(ω>0),设函数f(x)=
),(ω>0),设函数f(x)=![]()
![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求函数f(x)的表达式;
(2)求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本.法国的20本.日本的40本.犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国.礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:
(1)估计在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求恰有1名读书者年龄在
的读书者中任取2名,求恰有1名读书者年龄在![]() 的概率.
的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为![]() 元/件(
元/件(![]() ),则新增的年销量
),则新增的年销量![]() (万件).
(万件).
(1)写出今年商户甲的收益![]() (单位:万元)与
(单位:万元)与![]() 的函数关系式;
的函数关系式;
(2)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
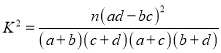
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com