
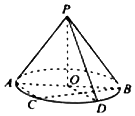
 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.分析 (Ⅰ)由AB是底面圆的直径,可得AC⊥BC.再由$\widehat{BC}$的中点为D,可得OD⊥BC.则AC∥OD.由线面平行的判定可得AC∥平面POD;
(Ⅱ)设圆锥底面圆半径为r,高为h,母线长为l,由题意可得h=r,l=$\sqrt{2}r$,由△PAB面积是9求得r=3,代入圆锥表面积公式与体积公式求解.
解答 (Ⅰ)证明:∵AB是底面圆的直径,∴AC⊥BC.
∵$\widehat{BC}$的中点为D,∴OD⊥BC.
又AC、OD共面,∴AC∥OD.
又AC?平面POD,OD?平面POD,
∴AC∥平面POD;
(Ⅱ)解:设圆锥底面圆半径为r,高为h,母线长为l,
∵圆锥的轴截面PAB为等腰直角三角形,∴h=r,l=$\sqrt{2}r$,
由${S}_{△ABP}=\frac{1}{2}×2r×h={r}^{2}=9$,得r=3,
∴${S}_{表面积}=πrl+π{r}^{2}=πr×\sqrt{2}r+π{r}^{2}=9(1+\sqrt{2})π$,
$V=\frac{1}{3}π{r}^{2}h=9π$.
点评 本题考查直线与平面平行的判定,考查圆锥表面积与体积的求法,考查空间想象能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
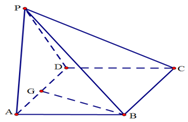 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com