
分析 由条件利用同角三角函数的基本关系的应用,诱导公式化简所给的式子可得结果.
解答 解:cos(α+$\frac{14π}{5}$)tan(α-$\frac{11π}{5}$)+$\frac{tan(α+\frac{9π}{5})}{cos(\frac{26π}{5}-α)}$=cos(α+$\frac{4π}{5}$)tan(α-$\frac{π}{5}$)+$\frac{tan(α-\frac{π}{5})}{cos(π+\frac{π}{5}-α)}$
=cos(π+α-$\frac{π}{5}$)tan(α-$\frac{π}{5}$)+$\frac{tan(α-\frac{π}{5})}{-cos(\frac{π}{5}-α)}$=-cos(α-$\frac{π}{5}$)tan(α-$\frac{π}{5}$)-$\frac{tan(α-\frac{π}{5})}{cos(α-\frac{π}{5})}$
=-sin(α-$\frac{π}{5}$)-$\frac{sin(α-\frac{π}{5})}{{cos}^{2}(α-\frac{π}{5})}$=-a-$\frac{a}{1{-a}^{2}}$.
点评 本题主要考查同角三角函数的基本关系的应用,诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.


科目:高中数学 来源: 题型:解答题
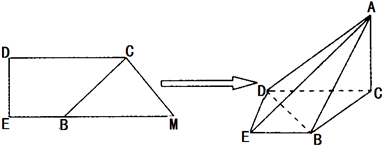
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,$\frac{1}{3}$) | C. | (-∞,-1)∪($\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上
已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.
设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com