
| A. | -8 | B. | -6 | C. | 4 | D. | 0 |
分析 利用已知条件以及向量的数量积化简求解即可.
解答 解:向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,
$\overrightarrow{b}$•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=$2\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{b}}^{2}$=2|$\overrightarrow{a}$||$\overrightarrow{b}$|cos60°-4=2×$2×2×\frac{1}{2}$-4=0.
故选:D.
点评 本题考查向量的数量积的运算,考查计算能力.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
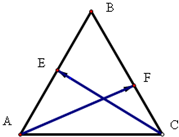 在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.
在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com