
分析 (1)根据函数解析式有意义,列不等式组求解.
(2)利用换元法求解函数的值域.
解答 解:(1)函数y=$\frac{{\sqrt{x+2}}}{x}$+(x-3)0
其定义域需满足:$\left\{\begin{array}{l}{x+2≥0}\\{x≠0}\\{x-3≠0}\end{array}\right.$.
解得:x≥-2且x≠0,x≠3.
∴函数y=$\frac{{\sqrt{x+2}}}{x}$+(x-3)0的定义域为{x|x≥-2且x≠0,x≠3}.
(2)函数y=2x-$\sqrt{x-1}$,
令t=$\sqrt{x-1}$,(t≥0),那么x=t2+1.
则函数y=2x-$\sqrt{x-1}$转化为f(t)=2(t2+1)-t.
整理得:f(t)=2t2-t+2.(t≥0)
根据二次函数的性质可知:
开口向上,对称轴t=$\frac{1}{4}$,
当t=$\frac{1}{4}$时,函数f(t)取得最小值为$\frac{15}{8}$.
∴函数y=2x-$\sqrt{x-1}$的值域为[$\frac{15}{8}$,+∞).
点评 本题考查了函数定义域求法就是列出函数解析式有意义的不等式组;考查了函数的值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | $[{0,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
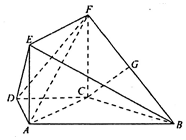 如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=-x2+1 | C. | y=|x|+1 | D. | y=$\sqrt{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com