
分析 (Ⅰ)由a1+a2+a3=6,a5=5求出数列{an}的公差即可;
(Ⅱ)${S_n}=1•{2^1}+2•{2^2}+3•{2^3}+…+n•{2^n}$…①,$2{S_n}=1•{2^2}+2•{2^3}+3•{2^4}+…+(n-1)•{2^n}+n•{2^{n+1}}$…②
利用错位相减法求和即可.
解答 解:(Ⅰ)∵数列{an}是等差数列,a1+a2+a3=6,∴3a2=6,即a2=2…(2分)
又a5=5∴数列{an}的公差$d=\frac{{{a_5}-{a_2}}}{3}=1$…(4分)∴a1=1…(5分)
∴数列{an}的通项公式为:an=n…(6分)
(Ⅱ)∵${b_n}={a_n}•{2^{a_n}},(n∈N*)$∴${b_n}=n•{2^n},(n∈N*)$…(7分)
∴${S_n}=1•{2^1}+2•{2^2}+3•{2^3}+…+n•{2^n}$…①
∴$2{S_n}=1•{2^2}+2•{2^3}+3•{2^4}+…+(n-1)•{2^n}+n•{2^{n+1}}$…②…(8分)
①-②得:$-{S_n}=2+{2^2}+{2^3}+…+{2^n}-n•{2^{n+1}}$…(9分)
∴${S_n}=n•{2^{n+1}}-\frac{{2•(1-{2^n})}}{1-2}$ …(10分)
∴${S_n}=n•{2^{n+1}}-2•({2^n}-1)=(n-1)•{2^{n+1}}+2$…(11分)
∴数列{bn}的前n项和${S_n}=(n-1)•{2^{n+1}}+2$.…(12分)
点评 本题考查了等差数列的通项,及错位相减法求和,属于基础题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $±\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{7}$ | D. | $±\frac{{4\sqrt{2}}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
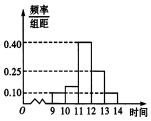 在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )
在“双11”促销活动中,某商场对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为14万元,则9时到11时的销售额为( )| A. | 3万元 | B. | 6万元 | C. | 8万元 | D. | 10万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com