
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足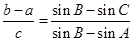 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.
(1)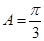 ;(2)
;(2)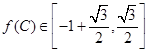 .
.
解析试题分析:本题主要考查解三角形中的正弦定理、余弦定理的应用、两角和与差的三角公式、函数的值域等数学知识,考查学生灵活运用数学公式的能力、转化能力以及计算能力.第一问,先利用正弦定理将角化为边,它类似于余弦定理的公式,再利用余弦定理求出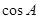 ,利用三角函数值在
,利用三角函数值在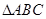 内求角,由于
内求角,由于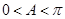 ,而
,而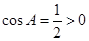 ,所以A为锐角;第二问,因为
,所以A为锐角;第二问,因为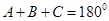 ,所以
,所以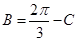 ,代入到解析式中,利用两角和与差的正余弦公式化简表达式,由于关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立,所以
,代入到解析式中,利用两角和与差的正余弦公式化简表达式,由于关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立,所以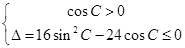 ,解出
,解出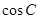 的取值范围,在
的取值范围,在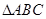 中解出角C的取值范围,将得到的角C的范围代入到
中解出角C的取值范围,将得到的角C的范围代入到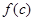 解析式中,求函数值域.
解析式中,求函数值域.
试题解析:(1)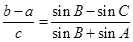
由正弦定理、余弦定理得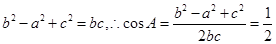 ,
,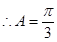 ,………6分
,………6分
(2)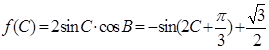 ,
,
∵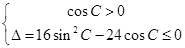
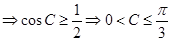
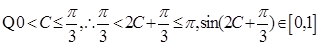
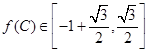 …12分
…12分
考点:1.正弦定理;2.余弦定理;3.两角和与差的正弦、余弦公式;4.函数值域.


科目:高中数学 来源: 题型:解答题
已知甲船正在大海上航行,当它位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即以10海里/小时的速度匀速前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: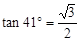 ).
).
(1)试问乙船航行速度的大小;
(2)试问乙船航行的方向(试用方位角表示,如北偏东…度).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知m=(2cos x+2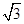 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设A、B两点在河的两岸,一测量者在A所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°,求A、B两点的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com