
| A. | 0 | B. | 1 | C. | 2 | D. | 6 |
分析 本题要求的是函数最大值与最小值的和,由函数的解析式,可通过研究函数的对称性来探究解题的思路,故可先求出f(-x),再与函数f(x)=1+sinx-x进行比较,总结规律,再由本题中所求的m+n的值是一个定值,采用特殊值法求出答案.
解答 解:∵f(x)=1+sinx-x
∴f(-x)=1-sinx+x
f(x)+f(-x)=2…①
又本题中f(x)=1+sinx-x
在区间[-6,6]上的值域为[m,n],
即无论x取什么样的实数都应有最大值与最小值的和是一个确定的值,
∴可令x=k,故m+n=f(k)+f(-k).
由①知,m+n=f(k)+f(-k)=2.
故选C
点评 本题是双重函数问题,一个隐蔽的函数性成立的问题,sinx是周期性函数,解题的关键一是意识到m+n是一个定值,再就是根据所给区间[-6,6]关于原点对称,联想到研究f(x)+f(-x)的值,这是本题解题的重点,难点是领会到m+n是一个定值,本题考查了推理判断的能力,比较抽象,注意领会本题做题中的经验技巧和发散思维.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{2}$或$\frac{2}{3}$ | D. | -$\frac{2}{3}$或-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
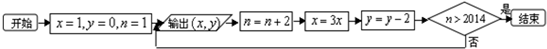
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com