
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
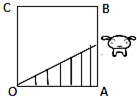 如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )
如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )A、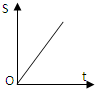 |
B、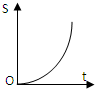 |
C、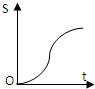 |
D、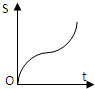 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com