
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
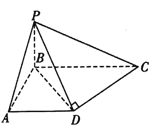
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置,若不存在,说明理由.
上的位置,若不存在,说明理由.
【答案】(1)见解析;(2)![]() ;(3)存在这样的
;(3)存在这样的![]() 点,
点, ![]() 为棱
为棱![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证
,即证![]() 平面
平面![]() ;
;
(2)以为![]() 原点,
原点, ![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系,求面
轴,建立空间直角坐标系,求面![]() 的法向量,利用向量求线面角即可;
的法向量,利用向量求线面角即可;
(3)假设存在,设![]() ,利用法向量求平面
,利用法向量求平面![]() 与平面
与平面![]() 所成角即可.
所成角即可.
试题解析:
(1) ![]() 底面
底面![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() .
.

(2)如图,以为![]() 原点,
原点, ![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系,由(1)易知
轴,建立空间直角坐标系,由(1)易知![]() 是等腰直角三角形,
是等腰直角三角形, ![]() .设
.设![]() ,则
,则![]() ,则
,则![]() ,因为异面直线
,因为异面直线![]() 和
和![]() 所成角等于
所成角等于![]() ,
, 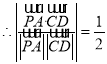 ,即
,即![]() ,解得
,解得![]() .设平面
.设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由 ,得
,得![]() ,所以可取
,所以可取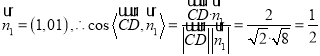 ,所以直线
,所以直线![]() 和平面
和平面![]() 所成的正弦值为
所成的正弦值为![]() .
.
(3)假设存在,设![]() ,且
,且![]() ,则
,则![]() ,设平面
,设平面![]() 一个法向量为
一个法向量为![]() ,则由
,则由 ,得
,得![]() ,取
,取![]() ,又平面
,又平面![]() 的法向量为
的法向量为![]() ,由平面
,由平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ,可知余弦值为
,可知余弦值为![]() ,由
,由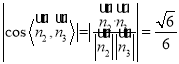 ,解得
,解得![]() 或
或![]() (不合题意).
(不合题意).
所以存在这样的![]() 点,
点, ![]() 为棱
为棱![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣![]() ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过35微克/立方米,
的年平均浓度不得超过35微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天
的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
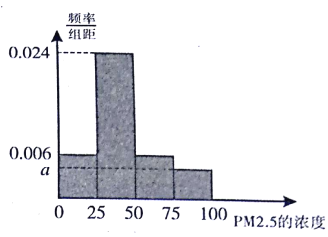
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)由频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n﹣5an﹣85,n∈N+ .
(1)求an .
(2)求数列{Sn}的通项公式,并求出n为何值时,Sn取得最小值?并说明理由.(参考数据:lg 2≈0.3,lg 3≈0.48).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( ) 
A.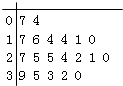
B.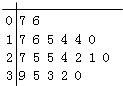
C.
D.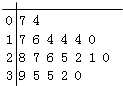
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 、
、![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,生产每吨
吨,生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过
吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过![]() 吨、
吨、![]() 吨、
吨、![]() 吨,如果
吨,如果![]() 产品的利润为
产品的利润为![]() 元/吨,
元/吨, ![]() 产品的利润为
产品的利润为![]() 元/吨,则该颜料公司一天内可获得的最大利润为( )
元/吨,则该颜料公司一天内可获得的最大利润为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com