
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过35微克/立方米,
的年平均浓度不得超过35微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天
的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
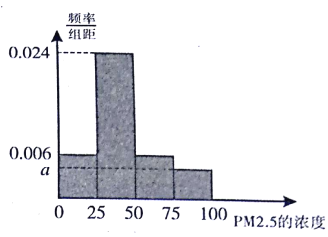
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)由频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ).
).
(1)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的极值点;
的极值点;
(3)令![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上相异三点,其中
上相异三点,其中![]() .求证:
.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2, cosC=![]() .
.
(I) 求△ABC的周长; (II)求cos(A﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为3x+4y﹣12=0,求直线l'的方程,使得:
(1)l'与l平行,且过点(﹣1,3);
(2)l'与l垂直,且l'与两轴围成的三角形面积为4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: 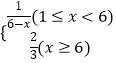 .(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
.(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量x为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
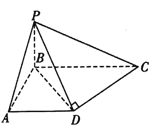
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置,若不存在,说明理由.
上的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 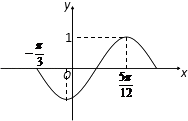
(1)求f(x)> ![]() 在x∈[0,π]上的解集;
在x∈[0,π]上的解集;
(2)设g(x)=2 ![]() cos2x+f(x),g(α)=
cos2x+f(x),g(α)= ![]() +
+ ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求sin2α的值.
),求sin2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河北省衡水中学2017届高三上学期五调】已知椭圆![]() ,圆
,圆![]() 的圆心
的圆心![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
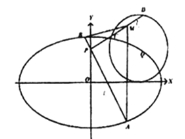
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交圆
交圆![]() 于
于![]() 两点,且
两点,且![]() 为
为![]() 的中点,求
的中点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com